��Ŀ����
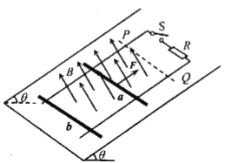
����Ŀ����ͼ��ʾ�������Ϊ30���б���ϵ�P�㶤��һ�⻬С��������P������ˮƽ���߽�б��һ��Ϊ�����ϲ��⻬���²��ֲڣ�һ����Ϊ3R����һ��ϵ��б��O�㣬��һ��ϵһ����Ϊm��С���ֽ�������ֱС���A���ɾ�ֹ�ͷţ�С��ǡ���ܵ�һ��ͨ��Բ���˶�����ߵ�B�㣮��֪OA��б��ױ�ƽ�У�OP����Ϊ2R������б��ױߴ�ֱ����С���A��B���˶�������(����)

A. ����������![]() mgR
mgR
B. ��������2mgR
C. �˷�Ħ��������![]() mgR
mgR
D. ��е�ܼ���![]() mgR
mgR
���𰸡�D
��������
��С��Ϊ�о��Ķ�����С��ǡ���ܵ�һ��ͨ��Բ���˶�����ߵ�B��ʱ�����ӵ�����Ϊ0��С���ܵ�������б���֧������������б�����µķ���ǡ��ͨ�����������ã�![]() ��
��
���ԣ�![]()
A��B�Ĺ����У�������Ħ������������Ħ��������ΪW����![]() ����
����
���ԣ�![]() ����
����
�������������ڶ��ܵ����ӣ�Ϊ��![]() ����A�����ɹ�ʽ��֪������˷�Ħ��������Ϊ0.25mgR�����Ի�е����ʧΪ0.25mgR����B����D��ȷ������������WG��mgRsin30�㣽
����A�����ɹ�ʽ��֪������˷�Ħ��������Ϊ0.25mgR�����Ի�е����ʧΪ0.25mgR����B����D��ȷ������������WG��mgRsin30�㣽![]() mgR����C����ѡD.
mgR����C����ѡD.

��ϰ��ϵ�д�
�����Ŀ