题目内容
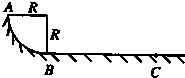 如图所示,半径R=1m的
如图所示,半径R=1m的| 1 | 4 |
(1)小木块到达圆弧轨道上B点时对轨道的压力;
(2)小木块在圆弧轨道上克服摩擦力做的功;
(3)BC段轨道的动摩擦因数为多少.
分析:(1)根据牛顿第二定律,通过径向的合力提供向心力求出支持力的大小,从而得出木块对B点的压力大小.
(2)对A到B的过程运用动能定理,求出小木块在圆弧轨道上克服摩擦力做功的大小.
(3)对BC段运用动能定理,求出BC段轨道的动摩擦因数的大小.
(2)对A到B的过程运用动能定理,求出小木块在圆弧轨道上克服摩擦力做功的大小.
(3)对BC段运用动能定理,求出BC段轨道的动摩擦因数的大小.
解答:解:(1)设轨道对小木块的支持力为N,则N-mg=m
.
代入数据解得N=38N
由牛顿第三定律可知,小木块对轨道的压力大小为38N,方向竖直向下.
(2)设小木块从A到B的过程中克服阻力做功为Wf,由动能定理得,
mgR-Wf=
mvB2
代入数据解得Wf=11J.
(3)设BC段轨道的动摩擦因数为μ,对BC段运用动能定理得,
-μmgsBC=0-
mvB2
代入数据解得μ=0.15.
答:(1)小木块到达圆弧轨道上B点时对轨道的压力为38N.
(2)小木块在圆弧轨道上克服摩擦力做的功为11J.
(3)BC段轨道的动摩擦因数为0.15.
| ||
| R |
代入数据解得N=38N
由牛顿第三定律可知,小木块对轨道的压力大小为38N,方向竖直向下.
(2)设小木块从A到B的过程中克服阻力做功为Wf,由动能定理得,
mgR-Wf=
| 1 |
| 2 |
代入数据解得Wf=11J.
(3)设BC段轨道的动摩擦因数为μ,对BC段运用动能定理得,
-μmgsBC=0-
| 1 |
| 2 |
代入数据解得μ=0.15.
答:(1)小木块到达圆弧轨道上B点时对轨道的压力为38N.
(2)小木块在圆弧轨道上克服摩擦力做的功为11J.
(3)BC段轨道的动摩擦因数为0.15.
点评:本题考查了动能定理和牛顿第二定律的综合运用,运用动能定理解题,关键选择好研究的过程,分析过程中有哪些力做功,然后结合动能定理列式求解.

练习册系列答案
相关题目
 如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向间的夹角θ=37°,另一端点C为轨道的最低点.C点右侧的水平路面上紧挨C点放置一木板,木板质量M=1kg,上表面与C点等高.质量m=1kg的物块(可视为质点)从空中A点以v0=1.2m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.已知物块与木板间的动摩擦因数μ1=0.2,木板与路面间的动摩擦因数μ2=0.05,取g=10m/s2.试求:
如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向间的夹角θ=37°,另一端点C为轨道的最低点.C点右侧的水平路面上紧挨C点放置一木板,木板质量M=1kg,上表面与C点等高.质量m=1kg的物块(可视为质点)从空中A点以v0=1.2m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.已知物块与木板间的动摩擦因数μ1=0.2,木板与路面间的动摩擦因数μ2=0.05,取g=10m/s2.试求: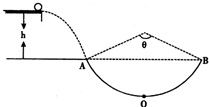 如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,其圆心角θ=106°,两端点A、B连线水平,质量为1㎏的小球自左侧平台上平抛后恰能无碰撞地从A点进入圆形轨道并沿轨道下滑.已知平台与AB连线高度差为h=0.8m(已知sin53°=0.8)
如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,其圆心角θ=106°,两端点A、B连线水平,质量为1㎏的小球自左侧平台上平抛后恰能无碰撞地从A点进入圆形轨道并沿轨道下滑.已知平台与AB连线高度差为h=0.8m(已知sin53°=0.8)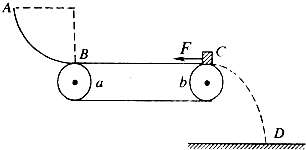
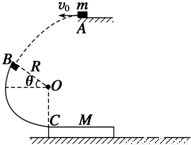 如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向间的夹角θ=37°,另一端点C为轨道的最低点.C点右侧的水平路面上紧挨C点放置一木板,木板质量M=l kg,上表面与C点等高.质量m=l kg的物块(可视为质点)从空中A点以v=1.2m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.已知物块与木板间的动摩擦因数μ1=0.2,木板与路面间的动摩擦,因数μ2=0.05.sin37°=0.6,cos37°=0.8,取g=10m/s2.试求:
如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向间的夹角θ=37°,另一端点C为轨道的最低点.C点右侧的水平路面上紧挨C点放置一木板,木板质量M=l kg,上表面与C点等高.质量m=l kg的物块(可视为质点)从空中A点以v=1.2m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.已知物块与木板间的动摩擦因数μ1=0.2,木板与路面间的动摩擦,因数μ2=0.05.sin37°=0.6,cos37°=0.8,取g=10m/s2.试求: