题目内容
 如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向间的夹角θ=37°,另一端点C为轨道的最低点.C点右侧的水平路面上紧挨C点放置一木板,木板质量M=1kg,上表面与C点等高.质量m=1kg的物块(可视为质点)从空中A点以v0=1.2m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.已知物块与木板间的动摩擦因数μ1=0.2,木板与路面间的动摩擦因数μ2=0.05,取g=10m/s2.试求:
如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向间的夹角θ=37°,另一端点C为轨道的最低点.C点右侧的水平路面上紧挨C点放置一木板,木板质量M=1kg,上表面与C点等高.质量m=1kg的物块(可视为质点)从空中A点以v0=1.2m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.已知物块与木板间的动摩擦因数μ1=0.2,木板与路面间的动摩擦因数μ2=0.05,取g=10m/s2.试求:(1)物块经过轨道上的C点时对轨道的压力大小;
(2)若木板足够长,请问从开始平抛至最终木板、物块都静止,整个过程产生的热量是多少?
分析:(1)物块从A到B做平抛运动,由平抛规律可求得B点的速度;由机械能守恒可求得C点的速度;由向心力公式可求得物块在C点受到的支持力,由牛顿第三定律可求得对轨道的压力;
(2)由能量守恒求出整个过程产生的热量.
(2)由能量守恒求出整个过程产生的热量.
解答:解:(1)设物体经过B点的速度为vB,则由平抛运动的规律可得:
vBsin37°=v0
解得,vB=2m/s
设物体经过C点的速度为vC,由机械能守恒得:
mvB2+mg(R+Rsin37°)=
mvC2
解得,vC=6m/s
物体经过C点时,设轨道对物块的支持力为FC,根据牛顿第二定律得:
Fc-mg=m
联立解得:Fc=46N;
由牛顿第三定律可知,物块经过圆轨道上的C点时对轨道的压力为46N;
(2)根据能量守恒得:整个过程产生的热量Q=
mvB2+mg(R+Rsin37°)=
×1×22+1×10×(1+0.6)=18J
答:
(1)物块经过轨道上的C点时对轨道的压力为46N;
(2)整个过程产生的热量为18J.
vBsin37°=v0
解得,vB=2m/s
设物体经过C点的速度为vC,由机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
解得,vC=6m/s
物体经过C点时,设轨道对物块的支持力为FC,根据牛顿第二定律得:
Fc-mg=m
| ||
| R |
联立解得:Fc=46N;
由牛顿第三定律可知,物块经过圆轨道上的C点时对轨道的压力为46N;
(2)根据能量守恒得:整个过程产生的热量Q=
| 1 |
| 2 |
| 1 |
| 2 |
答:
(1)物块经过轨道上的C点时对轨道的压力为46N;
(2)整个过程产生的热量为18J.
点评:题将平抛、圆周运动及直线运动结合在一起考查,注意分析运动过程,并根据过程正确的选择物理规律求解.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,其圆心角θ=106°,两端点A、B连线水平,质量为1㎏的小球自左侧平台上平抛后恰能无碰撞地从A点进入圆形轨道并沿轨道下滑.已知平台与AB连线高度差为h=0.8m(已知sin53°=0.8)
如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,其圆心角θ=106°,两端点A、B连线水平,质量为1㎏的小球自左侧平台上平抛后恰能无碰撞地从A点进入圆形轨道并沿轨道下滑.已知平台与AB连线高度差为h=0.8m(已知sin53°=0.8)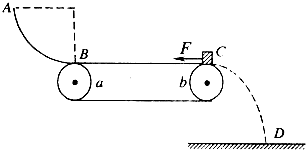
 如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向间的夹角θ=37°,另一端点C为轨道的最低点.C点右侧的水平路面上紧挨C点放置一木板,木板质量M=l kg,上表面与C点等高.质量m=l kg的物块(可视为质点)从空中A点以v=1.2m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.已知物块与木板间的动摩擦因数μ1=0.2,木板与路面间的动摩擦,因数μ2=0.05.sin37°=0.6,cos37°=0.8,取g=10m/s2.试求:
如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向间的夹角θ=37°,另一端点C为轨道的最低点.C点右侧的水平路面上紧挨C点放置一木板,木板质量M=l kg,上表面与C点等高.质量m=l kg的物块(可视为质点)从空中A点以v=1.2m/s的速度水平抛出,恰好从轨道的B端沿切线方向进入轨道.已知物块与木板间的动摩擦因数μ1=0.2,木板与路面间的动摩擦,因数μ2=0.05.sin37°=0.6,cos37°=0.8,取g=10m/s2.试求: