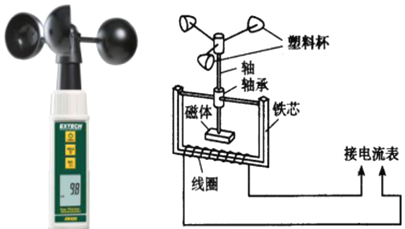
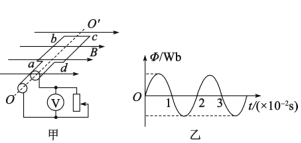
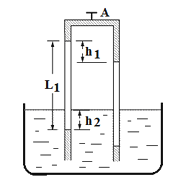
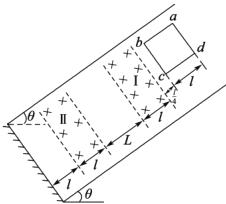
题目内容
【题目】如图所示,一玻璃砖的截面为直角三角形ABC,其中∠A =60°,AB=9cm。现有两细束平行且相同的单色光a、b,分别从AC边上的D点、E点以45°角入射,且均能从AB边上的F点射出,已知AD =AF= 3cm。求:
①玻璃砖的折射率;
②D、E两点之间的距离。

【答案】①![]() ;②12cm。
;②12cm。
【解析】
①光路图如图所示:
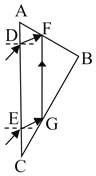
由于AD=AF,∠A=60°,则入射光a经AC边的折射角为:r=30°
玻璃砖的折射率为:
![]()
②设光在玻璃砖中发生全反射的临界角为C,则有:
![]()
则有:
C=45°
由图可知,b光经AC边折射后,在BC边上的入射角为60°,大于临界角C,所以此光线在G点发生了全反射.
由几何知识可知,四边形DEGF是平行四边形,由于
∠BFG=60°,
AF=3cm
则有:
BF=AB-AF=9cm-3cm=6cm
BF=FGcos60°
又
FG=DE
联立解得:
DE=12cm。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目