题目内容
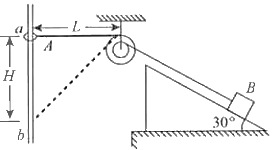
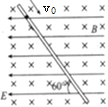
【题目】如图所示，空间中存在水平方向的匀强电场和匀强磁场，且电场方向和磁场方向相互垂直，在正交的电磁场空间中有一足够长的固定粗糙绝缘杆，与电场方向成60°夹角且处于竖直平面内，一质量为m，带电量为q（q＞0）的小球套在绝缘杆上，当小球沿杆向下的初速度为v0时，小球恰好做匀速直线运动，已知重力加速度大小为g，磁感应强度大小为B，电场强度大小为E=
，小球电荷量保持不变，则以下说法正确的是
A. 小球的初速度
B. 若小球沿杆向下的初速度为
，则小球将沿杆做加速度不断增大的减速运动，最后停止
C. 若小球沿杆向下的初速度为
，则小球将沿杆做加速度不断减小的减速运动，最后停止
D. 若小球沿杆向下的初速度为，则小球从开始运动到稳定过程中，克服摩擦力做功为
【答案】A
【解析】
本题是带电小球在复合场中的运动问题；对带电小球的受力情况和运动情况分析后，据平衡条件、牛顿第二定律、动能定理等知识列式求解。
A：带电小球受重力
、电场力
、磁场力及可能存在的支持力和摩擦力作用。重力与电场力的合力刚好与杆垂直，合力的大小为
；小球做匀速直线运动，磁场力的方向垂直于杆，则摩擦力、支持力均为0，磁场力与电场力、重力的合力相平衡，即
，解得：小球的初速度
。故A项正确。
B：若小球的初速度
，小球将受到重力、电场力、磁场力、支持力和摩擦力，据牛顿第二定律可得：
、
，解得：小球的加速度
，方向与小球的运动方向相反；所以小球做加速度减小的减速运动，最终匀速。故B项错误。
CD：若小球的初速度
，小球将受到重力、电场力、磁场力、支持力和摩擦力，据牛顿第二定律可得：
、，解得：小球的加速度
，方向与小球的运动方向相反；所以小球做加速度增大的减速运动，最终静止。小球从开始运动到稳定过程中，重力、电场力、磁场力、支持力四个力的合力与杆垂直，它们对小球做的功为0，摩擦力对小球做负功，据动能定理得
，所以小球从开始运动到稳定过程中，克服摩擦力做功为
。故CD两项错误。
