Question

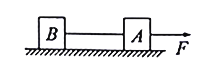
【题目】如图所示，木板A、B紧靠在一起，放在光滑水平面上，mA=5kg，mB=4kg，A、B上表面粗糙．另有一个质量为1kg的物块C以初速度v0从A的左端向右滑动，最后C物块在木板B上与木板B一起以1.5m/s的速度运动，木板A最终的速度大小为vA=0.5m/s．已知C与A、B间动摩擦因数均为μ=0.2，求：

（1）物块C的初速度v0的大小；

（2）物块C在木板B上滑行的距离．

Answer 1

【答案】（1）10m/s （2）5m

【解析】

(1)以A、B、C三个物块组成的系统为研究对象，当C在A、B上滑动时，A、B、C三个物块间存在相互作用，但在水平方向不存在其他外力作用，因此系统的动量守恒．

由动量守恒定律有mCv0=mAvA+（mB+mC）vB

解得：v0===10m/s

(2)C滑上B后与A分离，C、B系统在水平方向动量守恒．C离开A时C的速度为v1，B与A的速度同为vA，以B、C为系统，

由动量守恒定律有:mCv1+mBvA=（mB+mC）vB

v1===5.5m/s

对C在B上滑动过程，

由能量转化与守恒定律有：-

代值解得：L=5m