题目内容
 风洞实验室中可以产生水平方向的、大小可调节的风力.现将一套有小球的光滑细杆AB放入风洞实验室,小球孔径略大于细杆直径,细杆与水平方向夹角37°并固定.现产生水平向右,大小为小球所受重力0.8倍的风,让小球从细杆底部A端由静止开始运动.已知小球质量m,重力加速度g,细杆长L,求:
风洞实验室中可以产生水平方向的、大小可调节的风力.现将一套有小球的光滑细杆AB放入风洞实验室,小球孔径略大于细杆直径,细杆与水平方向夹角37°并固定.现产生水平向右,大小为小球所受重力0.8倍的风,让小球从细杆底部A端由静止开始运动.已知小球质量m,重力加速度g,细杆长L,求:?(1)小球从细杆A端滑到B端风力做的功;
(2)小球从细杆A端滑到B端风力的平均功率.
??
分析:(1)已知风的作用力与小球的位移,由功的计算公式可以求出风力做的功;
(2)由牛顿第二定律求出小球的加速度,求出小球的运动时间,然后由功率公式求出风力的平均功率.
(2)由牛顿第二定律求出小球的加速度,求出小球的运动时间,然后由功率公式求出风力的平均功率.
解答:解:(1)风力为重力的0.8倍,则风力F=0.8mg,
小球从A端滑动B端,风力做功:
W=FLcos37°=0.8mg×L×0.8=0.64mgL;
(2)由牛顿第二定律得:0.8mgcos37°-mgsin37°=ma,
解得:a=0.04g,
小球做匀加速直线运动,由匀变速运动的位移公式得:
L=
at2,小球的运动时间:t=
=
=5
,
风力做功的平均公式:
P=
=
=0.064mg
;
答:(1)小球从细杆A端滑到B端风力做的功为0.64mgL;
(2)小球从细杆A端滑到B端风力的平均功率为0.064mg
.
小球从A端滑动B端,风力做功:
W=FLcos37°=0.8mg×L×0.8=0.64mgL;
(2)由牛顿第二定律得:0.8mgcos37°-mgsin37°=ma,
解得:a=0.04g,
小球做匀加速直线运动,由匀变速运动的位移公式得:
L=
| 1 |
| 2 |
|
|
|
风力做功的平均公式:
P=
| W |
| t |
| 0.64mgL | ||||
5
|
| 2gL |
答:(1)小球从细杆A端滑到B端风力做的功为0.64mgL;
(2)小球从细杆A端滑到B端风力的平均功率为0.064mg
| 2gL |
点评:本题考查了求功与功率问题,应用功的计算公式、牛顿第二定律、运动学公式、功率公式即可正确解题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 选做题
选做题
 风洞实验室中可以产生水平方向、风速大小可以调节的风.现将一个套有小球的细直杆放入风洞实验室,小球的质量是m=1kg,球的孔径略大于细杆的直径,小球与杆的动摩擦因数是μ=0.8.
风洞实验室中可以产生水平方向、风速大小可以调节的风.现将一个套有小球的细直杆放入风洞实验室,小球的质量是m=1kg,球的孔径略大于细杆的直径,小球与杆的动摩擦因数是μ=0.8.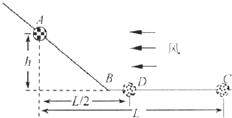 风洞实验室在航空航天飞行器的研究中发挥着重要的作用,用它可以分析、研究影响飞行器飞行速度的各种因素.风洞实验室中可以产生方向水平、速度大小可调节的风,用来研究处在流动气体中物体的受力情况.现将一套有木球的细折杆ABC固定在风洞实验中,球的质量为m,重力加速度为g,球在杆上运动时,球与杆之间的滑动摩擦力跟它们之间的弹力成正比,比例系数为k,设AB、BC的交接处B点用一段小圆弧平滑连接(即认为小球过B点的瞬间速度大小会突然变化),如图所示.
风洞实验室在航空航天飞行器的研究中发挥着重要的作用,用它可以分析、研究影响飞行器飞行速度的各种因素.风洞实验室中可以产生方向水平、速度大小可调节的风,用来研究处在流动气体中物体的受力情况.现将一套有木球的细折杆ABC固定在风洞实验中,球的质量为m,重力加速度为g,球在杆上运动时,球与杆之间的滑动摩擦力跟它们之间的弹力成正比,比例系数为k,设AB、BC的交接处B点用一段小圆弧平滑连接(即认为小球过B点的瞬间速度大小会突然变化),如图所示.