题目内容
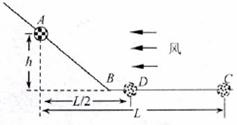
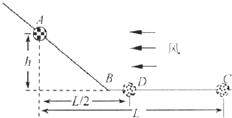 风洞实验室在航空航天飞行器的研究中发挥着重要的作用,用它可以分析、研究影响飞行器飞行速度的各种因素.风洞实验室中可以产生方向水平、速度大小可调节的风,用来研究处在流动气体中物体的受力情况.现将一套有木球的细折杆ABC固定在风洞实验中,球的质量为m,重力加速度为g,球在杆上运动时,球与杆之间的滑动摩擦力跟它们之间的弹力成正比,比例系数为k,设AB、BC的交接处B点用一段小圆弧平滑连接(即认为小球过B点的瞬间速度大小会突然变化),如图所示.
风洞实验室在航空航天飞行器的研究中发挥着重要的作用,用它可以分析、研究影响飞行器飞行速度的各种因素.风洞实验室中可以产生方向水平、速度大小可调节的风,用来研究处在流动气体中物体的受力情况.现将一套有木球的细折杆ABC固定在风洞实验中,球的质量为m,重力加速度为g,球在杆上运动时,球与杆之间的滑动摩擦力跟它们之间的弹力成正比,比例系数为k,设AB、BC的交接处B点用一段小圆弧平滑连接(即认为小球过B点的瞬间速度大小会突然变化),如图所示.实验时,先在无风的情况下让小球从斜杆上h高处由静止释放,小球最后滑到水平面上的C点停下,测得AC两点间水平距离为L1;接着调节合适的风速大小,再将小球从杆的上端同一位置由静止释放,小球最后停在水平面上的D点,测得AD两点间水平距离为
| L | 2 |
(1)比例系数k值的大小;
(2)水平风力F多大?
(3)若斜面的倾角θ为已知,要使小球在杆上保持静止状态,水平风力F必须满足什么条件?(设最大静摩擦力与滑动摩擦力相等)
分析:根据球与杆之间的摩擦力与压力成正比,比例系是k,可以列出关系式:f=kF压,当杆水平放置时,压力等于球的重力G,根据关系式推出摩擦力大小,风力大小等于摩擦力
解答:解:(1)因为球在杆上运动时,球与杆之间的滑动摩擦力跟它们之间的弹力成正比,设比例系数为k,并设AB间的水平距离为x,斜面的倾角为θ,无风时,小球从A点到C点,根据动能定理得:
mgh-kmgcosθ?
-kmg(L-x)=0
解得:k=
(2)有风时,小球从A点到D点,根据动能定理得:mgh-F?
-k(mgcosθ+Fsinθ)?
-kmg(
-x)=0(其中xtanθ=h)
解得:F=
mg=
mg
(3)小球沿斜面有上滑趋势时:Fmaxcosθ=mgsinθ+k(mgcosθ+Fmaxsinθ)
解得:Fmax=
?mg
小球沿斜面有下滑趋势时:Fmincosθ=mgsinθ-k(mgcosθ+Fminsinθ)
解得:Fmin=
?mg
所以风力大小的范围是:
?mg≤F≤
?mg
答:(1)比例系数k值的大小为
;
(2)水平风力F为
mg;
(3)若斜面的倾角θ为已知,要使小球在杆上保持静止状态,水平风力F必须满足:
?mg≤F≤
?mg.
mgh-kmgcosθ?
| x |
| cosθ |
解得:k=
| h |
| L |
(2)有风时,小球从A点到D点,根据动能定理得:mgh-F?
| L |
| 2 |
| x |
| cosθ |
| L |
| 2 |
解得:F=
| 2h-kL |
| 2kh+L |
| hL |
| 2h2+L2 |
(3)小球沿斜面有上滑趋势时:Fmaxcosθ=mgsinθ+k(mgcosθ+Fmaxsinθ)
解得:Fmax=
| Lsinθ+hcosθ |
| Lcosθ-hsinθ |
小球沿斜面有下滑趋势时:Fmincosθ=mgsinθ-k(mgcosθ+Fminsinθ)
解得:Fmin=
| Lsinθ-hcosθ |
| Lcosθ+hsinθ |
所以风力大小的范围是:
| Lsinθ-hcosθ |
| Lcosθ+hsinθ |
| Lsinθ+hcosθ |
| Lcosθ-hsinθ |
答:(1)比例系数k值的大小为
| h |
| L |
(2)水平风力F为
| hL |
| 2h2+L2 |
(3)若斜面的倾角θ为已知,要使小球在杆上保持静止状态,水平风力F必须满足:
| Lsinθ-hcosθ |
| Lcosθ+hsinθ |
| Lsinθ+hcosθ |
| Lcosθ-hsinθ |
点评:本题解题的关键:①物体匀速直线运动时,二力平衡,大小相等;②会根据题意列出摩擦力与压力的关系式.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目