题目内容
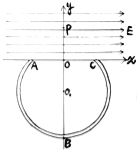
【题目】两个相同的全长电阻为9 Ω、半径为8cm的均匀光滑圆环固定在一个绝缘的水平台面上,两环分别在两个互相平行的、相距为20 cm的竖直面内,两环的圆心连线恰好与环面垂直,两环面间有方向竖直向下的磁感应强度B= ![]() T的匀强磁场(未画出),两环的最高点A和C间接有一内阻为0.5 Ω的电源,连接的导线的电阻不计.今有一根质量为10 g、电阻为1.5 Ω的棒置于两环内侧且可沿环滑动,而棒恰好静止于如图所示的水平位置,它与圆弧的两接触点P、Q和圆弧最低点间所夹的弧对应的圆心角均为θ=60°,重力加速度g取10 m/s2.试求:
T的匀强磁场(未画出),两环的最高点A和C间接有一内阻为0.5 Ω的电源,连接的导线的电阻不计.今有一根质量为10 g、电阻为1.5 Ω的棒置于两环内侧且可沿环滑动,而棒恰好静止于如图所示的水平位置,它与圆弧的两接触点P、Q和圆弧最低点间所夹的弧对应的圆心角均为θ=60°,重力加速度g取10 m/s2.试求:
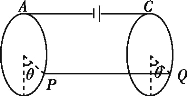
(1)此电源电动势E的大小.
(2)若换上两个电阻可忽略的光滑圆环和电动势E的大小为2V的电源,其他条件不变,现将棒从圆环最低点静止释放,问:棒经过P、Q点时对两环的弹力各为多少?棒能上升的最大高度?
【答案】(1)E=6 V.(2)0.2N 12cm
【解析】
(1)从左向右看,棒PQ的受力如图所示,棒受重力mg、安培力F安和环对棒的弹力FN作用;
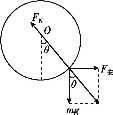
根据平衡条件得F安=mgtanθ,
安培力F安=IBL,
联立解得I=1 A,
在电路中两个圆环分别连入电路的电阻为R环=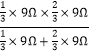 =2 Ω;
=2 Ω;
由闭合电路欧姆定律得:E=I(r+2R环+R棒)=6 V.
(2)若换上两个电阻可忽略的光滑圆环和电动势E的大小为2V的电源,则电路中的电流![]()
安培力F安1=BI1L=![]() N
N
棒经过P、Q点时的速度为v,则![]()
解得:v=![]() m/s;
m/s;
棒在经过P、Q点时,由牛顿第二定律:![]()
解得FN1=0.2N
棒在平衡位置的速度最大,此位置的与圆心的连线与竖直方向的夹角为![]() ,则α=600,
,则α=600,
则棒能上升的最高点应该关于平衡位置对称,则棒能上升的最大高度为h=R(1+cos600)=12cm

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目