题目内容
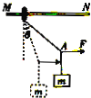
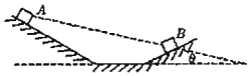
【题目】所示,木块从左边斜面的A点自静止开始下滑,经过一段水平面后,又滑上右边斜面并停留在B点。若木块与接触面间的动摩擦因数处处相等,AB连线与水平面夹角为θ,不计木块在路径转折处碰撞损失的能量,则( )
A. 木块与接触面间的动摩擦因数为![]()
B. 木块与接触面间的动摩擦因数为![]()
C. 左边斜面的倾角一定大于![]()
D. 右边斜面的倾角一定不大于![]()
【答案】BCD
【解析】
AB、设AB间的水平分位移为x,高度差为h,如图所示:
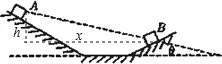
对从A到B间的过程运用动能定理,有:![]() ,其中:
,其中:![]() ,联立解得:
,联立解得:![]() ,故A错误,B正确;
,故A错误,B正确;
CD、对左侧斜面,木块要能够滑下来,重力的下滑分力要大于滑动摩擦力,则:mgsinα>μmgcosα,动摩擦因数:μ=tanθ,解得:α>θ,对于右侧斜面,木块不能滑下,故重力的下滑分力要不大于滑动摩擦力,故:mgsinβ≤μmgcosβ,由于μ=tanθ,故:β≤θ,故CD正确。

练习册系列答案
相关题目