题目内容
17.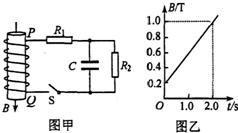 在如图甲所示的电路中,螺线管匝数n=1500匝,横截面积S=20cm2.螺线管导线电阻r=1.0Ω,R1=4.0Ω,R2=5.0Ω,C=30μF,P、Q为螺线管两端点.在一段时间内,穿过螺线管的磁场的磁感应强度B方向如图甲所示,大小按如图乙所示的规律变化.求该段时间内:
在如图甲所示的电路中,螺线管匝数n=1500匝,横截面积S=20cm2.螺线管导线电阻r=1.0Ω,R1=4.0Ω,R2=5.0Ω,C=30μF,P、Q为螺线管两端点.在一段时间内,穿过螺线管的磁场的磁感应强度B方向如图甲所示,大小按如图乙所示的规律变化.求该段时间内:(1)螺线管感应电动势的大小及P,Q两点哪一点电势高
(2)电容器两极板的带电量.
分析 根据法拉第电磁感应定律求出螺线管中感应电动势的大小,结合楞次定律得出感应电流的方向,从而比较出P、Q两点的电势.
根据闭合电路欧姆定律求出电容器两端的电压,根据Q=CU求出电容器两极板的电荷量.
解答 解:(1)感应电动势E=$n\frac{△BS}{△t}=1500×\frac{1-0.2}{2}×20×1{0}^{-4}V$=1.2V.
根据楞次定律知,电流的方向在螺线管中由P到Q,可知Q的电势高于P点的电势.
(2)电路中的电流I=$\frac{E}{{R}_{1}+{R}_{2}+r}=\frac{1.2}{4+5+1}A=0.12A$,
则电容器两端的电压U=IR2=0.12×5V=0.6V,
则电容器两极板的电荷量Q=CU=30×10-6×0.6C=1.8×10-5C.
答:(1)螺线管感应电动势的大小为1.2V,Q的电势高于P点的电势.
(2)电容器两极板的带电量为1.8×10-5C.
点评 本题考查了法拉第电磁感应定律和电路的综合运用,会根据楞次定律判断感应电流的方向,注意螺线管相当于电源,内部电流由负极流向正极.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
12. 如图所示,一导线弯成的闭合线圈(尺寸如图,右侧部分为半径为r的半圆),在纸面内以水平速度v向左匀速进入磁感应强度为B的匀强磁场,磁场方向垂直纸面向外.线圈总电阻为R,从线圈进入磁场开始到完全进入磁场为止,下列结论正确的是( )
如图所示,一导线弯成的闭合线圈(尺寸如图,右侧部分为半径为r的半圆),在纸面内以水平速度v向左匀速进入磁感应强度为B的匀强磁场,磁场方向垂直纸面向外.线圈总电阻为R,从线圈进入磁场开始到完全进入磁场为止,下列结论正确的是( )
 如图所示,一导线弯成的闭合线圈(尺寸如图,右侧部分为半径为r的半圆),在纸面内以水平速度v向左匀速进入磁感应强度为B的匀强磁场,磁场方向垂直纸面向外.线圈总电阻为R,从线圈进入磁场开始到完全进入磁场为止,下列结论正确的是( )
如图所示,一导线弯成的闭合线圈(尺寸如图,右侧部分为半径为r的半圆),在纸面内以水平速度v向左匀速进入磁感应强度为B的匀强磁场,磁场方向垂直纸面向外.线圈总电阻为R,从线圈进入磁场开始到完全进入磁场为止,下列结论正确的是( )| A. | 感应电流一直沿逆时针方向 | |
| B. | 线圈受到的安培力先增大,后减小 | |
| C. | 感应电动势的最大值E=Brv | |
| D. | 通过线圈某个横截面的电荷量为$\frac{{B({r^2}+π{r^2})}}{R}$ |
2.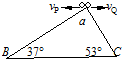 如图,在斜面块的顶角a处把两个小球P和Q以大小相同、方向相反的初速水平抛出,两球分别落到倾角为37°的斜面ab和倾为53°的斜面ac上,若不计空气阻力,则P、Q两球在空中运动的时间之比tP:tQ为( )
如图,在斜面块的顶角a处把两个小球P和Q以大小相同、方向相反的初速水平抛出,两球分别落到倾角为37°的斜面ab和倾为53°的斜面ac上,若不计空气阻力,则P、Q两球在空中运动的时间之比tP:tQ为( )
 如图,在斜面块的顶角a处把两个小球P和Q以大小相同、方向相反的初速水平抛出,两球分别落到倾角为37°的斜面ab和倾为53°的斜面ac上,若不计空气阻力,则P、Q两球在空中运动的时间之比tP:tQ为( )
如图,在斜面块的顶角a处把两个小球P和Q以大小相同、方向相反的初速水平抛出,两球分别落到倾角为37°的斜面ab和倾为53°的斜面ac上,若不计空气阻力,则P、Q两球在空中运动的时间之比tP:tQ为( )| A. | 16:9 | B. | 9:16 | C. | 1:1 | D. | 4:3 |
9.小球作类平抛运动时,分在两个互相垂直方向上的分运动的图线可能是( )


| A. | a和b | B. | b和d | C. | a和d | D. | c和d |
6.在光滑绝缘的水平面上有一个不导电的弹簧,弹簧的两端分别与金属小球A、B相连,若A、B带上等量同种电荷,弹簧伸长x1,若让A、B所带电量都增为原来的2倍,弹簧的伸长量为x2,则x1与x2的关系是( )
| A. | x2=x1 | B. | x2=4x1 | C. | x2>4x1 | D. | x2<4x1 |
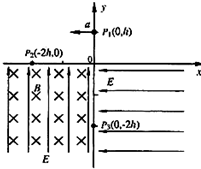 如图所示的坐标系中,x轴水平,y轴竖直,x轴上方空间只存在重力场,第Ⅲ象限存在沿y轴正方向的匀强电场和垂直xy平面向里的匀强磁场,在第Ⅳ象限有沿x轴负方向的匀强电场,场强与第Ⅲ象限存在的电场的场强大小相等.一质量为m,带电量为q的小球a,从轴上点P1(0,h)以一定的水平速度沿轴负方向抛出,它经过点P2(-2h,0)进入第Ⅲ象限,恰好做匀速圆周运动,又经过y轴上的点P3 (0,-2h)进入第Ⅳ象限,试求:
如图所示的坐标系中,x轴水平,y轴竖直,x轴上方空间只存在重力场,第Ⅲ象限存在沿y轴正方向的匀强电场和垂直xy平面向里的匀强磁场,在第Ⅳ象限有沿x轴负方向的匀强电场,场强与第Ⅲ象限存在的电场的场强大小相等.一质量为m,带电量为q的小球a,从轴上点P1(0,h)以一定的水平速度沿轴负方向抛出,它经过点P2(-2h,0)进入第Ⅲ象限,恰好做匀速圆周运动,又经过y轴上的点P3 (0,-2h)进入第Ⅳ象限,试求:
 如图所示为氢原子的能级图.现有大量处于n=4激发态的氢原子向低能级跃迁.
如图所示为氢原子的能级图.现有大量处于n=4激发态的氢原子向低能级跃迁.