题目内容
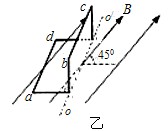
如图所示，“U”形金属框架固定在水平面上，处于竖直向下的匀强磁场中。现使ab棒突然获得一初速度V向右运动，下列说法正确的是 
| A．ab做匀减速运动 |
| B．回路中电流均匀减小 |
| C．a点电势比b点电势低 |
| D．安培力对ab棒做负功 |
D
解析试题分析：据题意，物体一旦运动就会产生电动势，即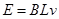
，在回路中产生电流，即：
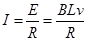，则导体棒将受到安培力，即：
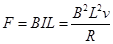，据牛顿第二定律有：
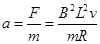，由于安培力做负功，则导体棒速度减小且加速度也减小，物体做加速度减小的减速运动，故A选项错误而D选项正确；速度非均匀减小，据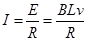可知电流也非均匀减小，故B选项错误；据右手定则可知，a端电势较高，故C选项错误。
考点：本题考查电磁感应。
如图所示，间距为l的光滑平行金属导轨与水平面夹角
30o，导轨电阻不计，正方形区域abcd内匀强磁场的磁感应强度为B，方向垂直导轨向上。甲、乙两金属杆电阻相同、质量均为m，垂直于导轨放置。起初甲金属杆处在磁场的上边界ab上，乙在甲上方距甲也为l处。现将两金属杆同时由静止释放，释放同时在甲金属杆上施加一个沿着导轨的拉力，使甲金属杆始终以大小为
的加速度沿导轨向下匀加速运动，已知乙金属杆刚进入磁场时做匀速运动，重力加速度为g，则以下正确的是
A．每根金属杆的电阻 |
| B．甲金属杆在磁场区域运动过程中，拉力对杆做的功在数值上等于电路中产生的焦耳热 |
C．乙金属杆在磁场区域运动过程中，安培力的功率是 |
D．乙金属杆进入磁场直至出磁场过程中回路中通过的电量为 |
如图所示，边长为L的正方形金属框，匝数为n,质量为m，电阻为R，用细线把它悬挂于一个有界的匀强磁场边缘，金属框的上半部处于磁场内，下半部处于磁场外．磁场随时间变化规律为B＝kt(k>0)，已知细线所能承受的最大拉力为2mg，下列说法正确的是（ ）
A．线圈的感应电动势大小为nk· |
| B．细绳拉力最大时，金属框受到的安培力大小为mg |
C．从t＝0开始直到细线会被拉断的时间为 |
| D．以上说法均不正确 |
如图所示，光滑导轨MN水平放置，两根导体棒平行放于导轨上，形成一个闭合回路，当一条形磁铁从上方下落(未达导轨平面)的过程中，导体P、Q的运动情况是： （ ）
| A．P、Q互相靠拢 |
| B．P、Q互相远离 |
| C．P、Q均静止 |
| D．因磁铁下落的极性未知，无法判断 |
如下图所示，两根光滑的金属导轨，平行放置在倾角为θ的斜面上，导轨的左端接有电阻R，导轨自身的电阻可忽略不计．斜面处在一匀强磁场中，磁场方向垂直于斜面向上．质量为m、电阻不计的金属棒ab，在沿着斜面与棒ab垂直的恒力F作用下沿导轨匀速上升，上升高度为h.则在此过程中，以下错误的是( )
| A．作用于棒ab上的各力的合力所做的功等于零 |
| B．恒力F和重力的合力所做的功等于电阻R上产生的焦耳热 |
| C．恒力F和安培力的合力所做的功等于零 |
| D．恒力F所做的功等于棒ab重力势能的增加量和电阻R上产生的焦耳热之和 |