题目内容
【题目】如图所示的竖直平面内,水平条形区域I和Ⅱ内有方向垂直竖直面向里的匀强磁场,其宽度均为d , I和Ⅱ之间有一宽度为h的无磁场区域,h>d。一质量为m、边长为d的正方形线框由距区域I上边界某一高度处静止释放,在穿过两磁场区域的过程中,通过线框的电流及其变化情况相同。重力加速度为g , 空气阻力忽略不计。则下列说法正确的是( )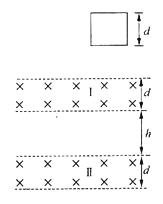
A.线框进入区域I时与离开区域I时的电流方向相同
B.线框进入区域Ⅱ时与离开区域Ⅱ时所受安培力的方向相同
C.线框有可能匀速通过磁场区域I
D.线框通过区域I和区域Ⅱ产生的总热量为Q=2mg(d+h)
【答案】B,D
【解析】由楞次定律可知,线框进入区域I时感应电流为逆时针方向,而离开区域I时的电流方向为顺时针方向,故选项A错误;
由楞次定律可知,线框进入区域Ⅱ时与离开区域Ⅱ时所受安培力的方向相同,均向上,选项B正确;
因穿过两磁场区域的过程中,通过线框的电流及其变化情况相同,则可知线圈进入磁场区域I一定是减速运动,选项C错误;
线圈出离磁场区域I的速度应等于出离磁场区域Ⅱ的速度,则在此过程中,线圈的机械能的减小量等于线圈通过产生区域Ⅱ产生的电能,即Q2= mg(d+h),则线框通过区域I和区域Ⅱ产生的总热量为Q=2Q2=2mg(d+h),选项D正确。
故选BD
本题考查楞次定律的理解和应用。楞次定律:感应电流具有这样的方向,即感应电流的磁场总要阻碍引起感应电流的磁通量的变化。

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目