题目内容
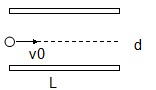
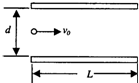一束质量为m、电量为q的带电粒子以平行于两极板的速度v0进入匀强电场，如图所示，如果两极板间电压为U，两极板间的距离为d，板长为L，设粒子束不会击中极板，则粒子从进入电场到飞出极板时电势能的变化量为分析：根据粒子在电场中受到电场力作用，导致粒子偏转，由运动学公式与牛顿第二定律可求出偏转位移y，并由W=qEy=q
y，即可求解．
| U |
| d |
解答：解：粒子在电场中做类平抛运动，
根据牛顿第二定律与运动学公式可得，
经过电场后的偏转位移y=
at2=
(
)2
而电场中，电势能的变化量等于电场力做功的多少，
即△E=W
又W= -qEy=-q
y
由以上两式，综合而得，
飞出极板时电势能的变化量为-
故答案为：-
根据牛顿第二定律与运动学公式可得，
经过电场后的偏转位移y=
| 1 |
| 2 |
| 1 |
| 2 |
| qU |
| md |
| L |
| v0 |
而电场中，电势能的变化量等于电场力做功的多少，
即△E=W
又W= -qEy=-q
| U |
| d |
由以上两式，综合而得，
飞出极板时电势能的变化量为-
| q2U2L2 | ||
2md2
|
故答案为：-
| q2U2L2 | ||
2md2
|
点评：本题运用动能定理研究带电粒子的电场中和复合场中的运动，列式时要抓住洛伦兹力不做功的特点．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
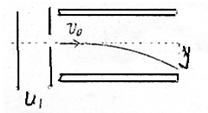如图所示，离子发生器发射出一束质量为m，电量为q的离子，从静止经过加速电压U1加速后，获得速度V0并沿垂直于电场方向射入两平行板中央，受偏转电压U2作用后，以速度v离开电场，已知平行板长为L，两板间的距离为d，求：
如图所示，在一半径为R的网形区域内有磁感应强度为B的匀强磁场，方向垂直纸面向外．一束质量为m、电量为q的带正电的粒子沿平行于直径MN的方向进入匀强磁场．粒子的速度大小不同，重力不计．入射点P到直径MN的距离为h，则：
