题目内容
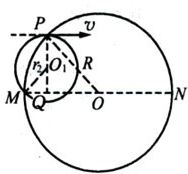
 如图所示,在一半径为R的网形区域内有磁感应强度为B的匀强磁场,方向垂直纸面向外.一束质量为m、电量为q的带正电的粒子沿平行于直径MN的方向进入匀强磁场.粒子的速度大小不同,重力不计.入射点P到直径MN的距离为h,则:
如图所示,在一半径为R的网形区域内有磁感应强度为B的匀强磁场,方向垂直纸面向外.一束质量为m、电量为q的带正电的粒子沿平行于直径MN的方向进入匀强磁场.粒子的速度大小不同,重力不计.入射点P到直径MN的距离为h,则:(1)某粒子经过磁场射出时的速度方向恰好与其入射方向相反,求粒子的入射速度是多大?
(2)恰好能从M点射出的粒子速度是多大?
(3)若h=
| R | 2 |
分析:先确定粒子半径然后由牛顿第二定律列方程求速度;
先画出粒子的运动轨迹,然后由几何知识确定出半径,然后根据牛顿第二定律列方程求速度;
先确定出圆心角,然后表示出周期公式,最后求时间.
先画出粒子的运动轨迹,然后由几何知识确定出半径,然后根据牛顿第二定律列方程求速度;
先确定出圆心角,然后表示出周期公式,最后求时间.
解答:解:(1)粒子出射方向与入射方向相反,在磁场中走了半周,其半径r1=h,
qv1B=m
所以v1=
(2)粒子从M点射出,其运动轨迹如图,在△MQO1中,
r22=(R-
)2+(h-r2)2
得:r2=
qv2B=
所以v2=
(3)若h=
,sin∠POQ=
,可得∠POQ=
由几何关系得粒子在磁场中偏转所对圆心角为α=
周期T=
所以t=
T=
答:(1)某粒子经过磁场射出时的速度方向恰好与其入射方向相反,粒子的入射速度是v1=
;
(2)恰好能从M点射出的粒子速度是
;
(3)若h=
,粒子从P点经磁场到M点的时间是
.
qv1B=m
| v12 |
| r1 |
所以v1=
| qBh |
| m |
(2)粒子从M点射出,其运动轨迹如图,在△MQO1中,

r22=(R-
| R2-h2 |
得:r2=
R2-R
| ||
| h |
qv2B=
| mv22 |
| r2 |
所以v2=
qBR(R-
| ||
| mh |
(3)若h=
| R |
| 2 |
| h |
| R |
| π |
| 6 |
由几何关系得粒子在磁场中偏转所对圆心角为α=
| 7π |
| 6 |
周期T=
| 2πm |
| qB |
所以t=
| α |
| 2π |
| 7πm |
| 6Bq |
答:(1)某粒子经过磁场射出时的速度方向恰好与其入射方向相反,粒子的入射速度是v1=
| qBh |
| m |
(2)恰好能从M点射出的粒子速度是
qBR(R-
| ||
| mh |
(3)若h=
| R |
| 2 |
| 7πm |
| 6Bq |
点评:考查了带电离子在磁场中的运动,会定圆心、找半径,结合圆周运动求相关量.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 如图所示,在一半径为50cm环形绝缘光滑细管处在着垂直纸面向里的匀强磁场中,磁感应强度为2.2T,管内有一个质量为10g的带电小球以6m/s的速度从管的最低点逆时针管中运动,运动到管的最高点时恰好对管没有作用力.
如图所示,在一半径为50cm环形绝缘光滑细管处在着垂直纸面向里的匀强磁场中,磁感应强度为2.2T,管内有一个质量为10g的带电小球以6m/s的速度从管的最低点逆时针管中运动,运动到管的最高点时恰好对管没有作用力. (2008?福建模拟)某离子速度选择器的原理示意图如图所示,在一半径为R=0.1m的圆柱筒内有B=1×10-2T的匀强磁场,方向平行于轴线,在圆柱筒截面某一直径两端筒壁上开有小孔a、b分别作为入射孔和出射孔.现有一束比荷
(2008?福建模拟)某离子速度选择器的原理示意图如图所示,在一半径为R=0.1m的圆柱筒内有B=1×10-2T的匀强磁场,方向平行于轴线,在圆柱筒截面某一直径两端筒壁上开有小孔a、b分别作为入射孔和出射孔.现有一束比荷
