题目内容
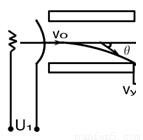
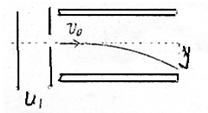 如图所示,离子发生器发射出一束质量为m,电量为q的离子,从静止经过加速电压U1加速后,获得速度V0并沿垂直于电场方向射入两平行板中央,受偏转电压U2作用后,以速度v离开电场,已知平行板长为L,两板间的距离为d,求:
如图所示,离子发生器发射出一束质量为m,电量为q的离子,从静止经过加速电压U1加速后,获得速度V0并沿垂直于电场方向射入两平行板中央,受偏转电压U2作用后,以速度v离开电场,已知平行板长为L,两板间的距离为d,求:(1)v0的大小;
(2)离子在偏转电场中运动的时间;
(3)离子在偏转电场受到的电场力的大小F
(4)离子在偏转电场中的加速度;
(5)离子在离开偏转电场时的横向偏移量y.
分析:粒子在加速电场中运动的过程中,电场力做功W=qU,根据动能定理求出离子的速度v0的大小;离子在偏转电场中做类平抛运动,水平方向匀速直线运动,竖直方向初速度为零的匀加速直线运动;电场力的大小为F=qE;根据牛顿第二定律解出离子在偏转电场中的加速度.
解答:解:(1)粒子在加速电场中运动的过程中,只有电场力做功W=qU,求出离子的速度v0的大小
根据动能定理得:qU1=
mv02,
解得:v0=
(2)离子在偏转电场中做类平抛运动,水平方向匀速直线运动,
所以:L=v0t
解得:t=
=L
(3)偏转电场的场强:E=
则电场力:F=qE=
(4)根据牛顿第二定律:qE=ma
解得:a=
(5)离子在偏转电场中做类平抛运动,竖直方向初速度为零的匀加速直线运动;
所以:y=
at2=
×
×
=
答:(1)v0的大小为
.;
(2)离子在偏转电场中运动的时间为L
;
(3)离子在偏转电场受到的电场力的大小为
;
(4)离子在偏转电场中的加速度
;
(5)离子在离开偏转电场时的横向偏移量
.
根据动能定理得:qU1=
| 1 |
| 2 |
解得:v0=
|
(2)离子在偏转电场中做类平抛运动,水平方向匀速直线运动,
所以:L=v0t
解得:t=
| L |
| v0 |
|
(3)偏转电场的场强:E=
| U 2 |
| d |
则电场力:F=qE=
| qU2 |
| d |
(4)根据牛顿第二定律:qE=ma
解得:a=
| qU2 |
| md |
(5)离子在偏转电场中做类平抛运动,竖直方向初速度为零的匀加速直线运动;
所以:y=
| 1 |
| 2 |
| 1 |
| 2 |
| qU2 |
| md |
| L2m |
| 2qU1 |
| U2L2 |
| 4dU1 |
答:(1)v0的大小为
|
(2)离子在偏转电场中运动的时间为L
|
(3)离子在偏转电场受到的电场力的大小为
| qU2 |
| d |
(4)离子在偏转电场中的加速度
| qU2 |
| md |
(5)离子在离开偏转电场时的横向偏移量
| U2L2 |
| 4dU1 |
点评:本题关键是分析清楚粒子的运动规律,对于类平抛运动,可以运用正交分解法分解为初速度方向的匀速直线运动和沿电场力方向的匀加速直线运动.

练习册系列答案
相关题目
 如图所示,离子发生器发射一束质量为m,电荷量为e,从静止经加速电压U1=5000v加速后,获得速度vo,并沿垂直于电场线方向射入两平行板中央,受偏转电压U2=400v作用后,以速度v离开电场,若两板间距离d=1.0cm,板长l=5.0cm,求:
如图所示,离子发生器发射一束质量为m,电荷量为e,从静止经加速电压U1=5000v加速后,获得速度vo,并沿垂直于电场线方向射入两平行板中央,受偏转电压U2=400v作用后,以速度v离开电场,若两板间距离d=1.0cm,板长l=5.0cm,求:
 ,并沿垂直于电场线方向射入两平行板中央,受偏转电压U2作用后,以速度
,并沿垂直于电场线方向射入两平行板中央,受偏转电压U2作用后,以速度 离开电场,已知平行板长为
离开电场,已知平行板长为 ,两板间距离为d,求:
,两板间距离为d,求: 

 和离子在离开偏转电场时的速度
和离子在离开偏转电场时的速度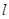 ,两板间距离为d.求:
,两板间距离为d.求: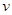 的大小和方向;
的大小和方向;