题目内容
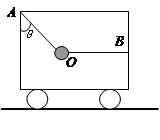
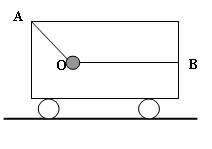
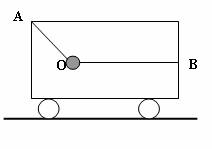
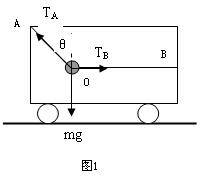如图，小车在水平面上以5m/s的速度向右做匀速直线运动，车厢内用OA、OB两细绳系住一个质量为2kg的物体，OA与竖直方向夹角为θ=37°，OB是水平的．后来小车改做匀减速运动，并经1.25m的位移停下来，求：
（1）车在匀速运动的过程中，两绳的拉力TA、TB各是多少？（sin37°=0.6）
（2）车在匀减速运动的过程中，两绳的拉力TA、TB各是多少？（g取10m/s2．）
解：（1）以小球为研究对象，小车匀速运动时其受力如图，根据平衡条件得
TAcosθ=mg①
TB=TAsinθ②
由①得，TA=
=
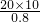N=25N
代入②得，TB=15N
（2）已知v0=5m/s，x=1.25m，v=0，由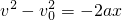
得
小车的加速度大小为a=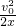
=
m/s2=10m/s2
当绳子恰好没有拉力时，设此时加速度为a0，根据牛顿第二定律得，
gtanθ=ma0，解得，a0=gtanθ=7.5m/s2＜a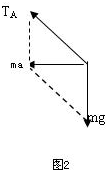
所以绳子OB已没有拉力，由图2得
TA=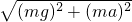
代入解得TA=28.2N
答：
（1）车在匀速运动的过程中，TA=25N，TB=15N．
（2）车在匀减速运动的过程中，TB=0，TA=28.2N．
分析：（1）小车匀速向右运动时，小球所受的合力为零，分析小球受力，根据平衡条件求出两绳的拉力TA、TB．
（2）车在向右匀减速运动的过程中，由初速度、位移和末速度求出加速度，再根据牛顿第二定律求出绳子OB拉力恰好为零时，小车的加速度，分析绳子OB是否有拉力，再求解TA、TB．
点评：本题第2问要注意分析绳子OB是否松驰，分析隐含的临界状态是难点．
TAcosθ=mg①
TB=TAsinθ②
由①得，TA=
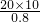=N=25N代入②得，TB=15N
（2）已知v0=5m/s，x=1.25m，v=0，由
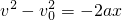得小车的加速度大小为a=
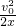=m/s2=10m/s2当绳子恰好没有拉力时，设此时加速度为a0，根据牛顿第二定律得，
gtanθ=ma0，解得，a0=gtanθ=7.5m/s2＜a
所以绳子OB已没有拉力，由图2得
TA=
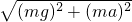
代入解得TA=28.2N
答：
（1）车在匀速运动的过程中，TA=25N，TB=15N．
（2）车在匀减速运动的过程中，TB=0，TA=28.2N．
分析：（1）小车匀速向右运动时，小球所受的合力为零，分析小球受力，根据平衡条件求出两绳的拉力TA、TB．
（2）车在向右匀减速运动的过程中，由初速度、位移和末速度求出加速度，再根据牛顿第二定律求出绳子OB拉力恰好为零时，小车的加速度，分析绳子OB是否有拉力，再求解TA、TB．
点评：本题第2问要注意分析绳子OB是否松驰，分析隐含的临界状态是难点．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
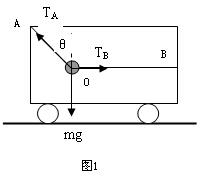如图，小车在水平面上以5m/s的速度向右做匀速直线运动，车厢内用OA、OB两细绳系住一个质量为2kg的物体，OA与竖直方向夹角为θ=37°，OB是水平的．后来小车改做匀减速运动，并经1.25m的位移停下来，求：
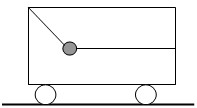如图，小车在水平面上以4m/s的速度向右做匀速直线运动，车厢内用OA、OB两细绳系住一个质量为2kg的物体，OA与竖直方向夹角为θ=37°，OB是水平的．后来小车改做匀减速运动，经8m的位移停下来（运动过程OB拉力不为0）．
