Question

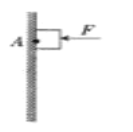
【题目】如图所示，质量为m可视为质点的物块锁定在足够长的竖直墙上的A点，物块与竖直墙面间动摩擦因数为μ。t=0时刻，在物块上施加一个水平向左的力F并同时解除锁定，F随时间的变化关系为F=kt（k为常数且大于零），重力加速为g，物块从开始运动到最后稳定状态的过程（ ）

A.t=时刻，物块的动量大小为

B.物块受到的摩擦力一直增大

C.t= 时刻，物块的速度最大

D.物块先做加速度减小的加速运动，然后做加速度增大的减速运动，最后做匀速运动

Answer 1

【答案】C

【解析】

A.在0—时间内，由动量定理得：

△p=mgt-

t=时刻，物块的动量大小

p=

选项A错误；

BC.物块受到的滑动摩擦力

f=Fμ=ktμ

当第一次

f=Fμ=ktμ=mg

即t=时刻，速度最大，后来摩擦力大，物块将减速下滑，当速度为零时，摩擦力突变为静摩擦力，根据平衡条件的最后静摩擦力等于重力，选项B错误、选项C正确；

D.根据牛顿第二定律有：

mg-Fμ=ma

得

a=10-5t

物块先做加速运动再做减速运动，加速度先减小再增大，最后速度减为零静止，选项D错误。