题目内容
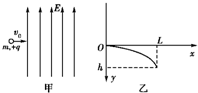一质量为m、带电荷量为+q的小球以水平初速度v0进入竖直向上的匀强电场中，如图甲所示．今测得小球进入电场后在竖直方向下降的高度y与水平方向的位移x之间的关系如图乙所示，根据图乙给出的信息，（重力加速度为g）求：（1）匀强电场场强的大小；
（2）小球从进入匀强电场到下降h高度的过程中，电场力做的功；
（3）小球在h高度处的动能．
分析：（1）小球做类平抛运动，由运动的合成与分解，根据水平方向的速度直线运动，竖直方向的匀加速直线运动可得出匀强电场的场强大小；
（2）由功的公式W=FL可求得电场力所做的功；
（3）由动能定理可得小球在高度h处的动能．
（2）由功的公式W=FL可求得电场力所做的功；
（3）由动能定理可得小球在高度h处的动能．
解答：解：（1）小球进入电场后，水平方向做匀速直线运动，设经过时间t，水平方向：v0t=L，
竖直方向：
=h
所以E=
-
．
（2）电场力做功为
W=-qEh=
．
（3）根据动能定理mgh-qEh=Ek-
得Ek=
+
．
答（1）匀强电场的场强为：
-
（2）电场力所做的功为
；
（3）
+
竖直方向：
| mg-qEpt2 |
| 2m |
所以E=
| mg |
| q |
2hm
| ||
| qL2 |
（2）电场力做功为
W=-qEh=
2h2m
| ||
| L2 |
（3）根据动能定理mgh-qEh=Ek-
m
| ||
| 2 |
得Ek=
2h2m
| ||
| L2 |
m
| ||
| 2 |
答（1）匀强电场的场强为：
| mg |
| q |
2hm
| ||
| q L2 |
2h2m
| ||
| L2 |
（3）
2h2m
| ||
| L2 |
m
| ||
| 2 |
点评：带电粒子在电场中的运动可分为加速和偏转，加速类的题目由动能定理求解，而偏转类的题目一般考查运动的合成与分解的应用．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
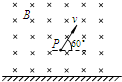如图所示，在水平地面上方附近有一范围足够大的互相正交的匀强电场和匀强磁场区域．磁场的磁感应强度为B，方向水平并垂直纸面向里．一质量为m、带电荷量为q的带正电微粒在此区域内沿竖直平面（垂直于磁场方向的平面）做速度大小为v的匀速圆周运动，重力加速度为g．
（2008?崇文区一模）如图所示，在水平地面上方附近有一范围足够大的互相正交的匀强电场和匀强磁场区域．磁场的磁感应强度为B，方向水平并垂直纸面向里．一质量为m、带电荷量为q的带正电微粒在此区域内沿竖直平面（垂直于磁场方向的平面）做速度大小为v的匀速圆周运动，重力加速度为g．
（2013?日照一模）如图所示，在直角坐标系xoy的第一、四象限区域内存在两个有界的匀强磁场：垂直纸面向外的匀强磁场I、垂直纸面向里的匀强磁场II，O、M、P、Q为磁场边界和x轴的交点OM=MP=L．在第三象限存在沿y轴正向的匀强电场．一质量为m、带电荷量为+q的粒子从电场中坐标为（-2L，-L）的点以速度υ0沿+x方向射出，恰好经过原点O处射入区域I又从M点射出区域I（粒子的重力忽略不计）．
如图所示，直线MN上方存在垂直纸面向里、磁感应强度大小为B的匀强磁场，现有一质量为m、带电荷量为+q的粒子在纸面内以某一速度从A点射入，其方向与MN成30°角，A点到MN的垂直距离为d，带电粒子重力不计．求：