题目内容
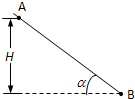如图，质量为m的小球A穿在光滑绝缘细杆上，杆的倾角为α，小球A带正电、电量为q，在杆上B点处固定一个电量为Q的正电荷，A、B间竖直高度为H，整个装置处在真空中．将小球A由静止释放，A下滑过程中电量保持不变，则球刚释放时的加速度大小为gsinα-
| kqQ(sinα)2 |
| mh2 |
gsinα-
；下滑过程中，当A球的动能最大时，A球与B点的距离为| kqQ(sinα)2 |
| mh2 |
|
|
分析：对A球受力分析，受到重力、支持力和静电斥力，根据牛顿第二定律求加速度；小球A先加速下滑，当静电斥力等于重力的下滑分量时，小球速度最大，之后减速下降，再加速返回，减速返回到最高点，完成一次振动，即在平衡位置速度最大．
解答：解：对小球受力分析，受到重力、支持力和静电斥力，根据牛顿第二定律，有
mgsinα-F=ma
根据库仑定律，有
F=k
解得
a=gsinα-
到达平衡位置时，速度最大，根据平衡条件，有
mgsinα-k
=0
解得
x=
mgsinα-F=ma
根据库仑定律，有
F=k
(
|
解得
a=gsinα-
| kqQ(sinα)2 |
| mh2 |
到达平衡位置时，速度最大，根据平衡条件，有
mgsinα-k
| x2 |
解得
x=
|
点评：本题关键对小球A受力分析，然后根据牛顿第二定律求解加速度，根据力与速度关系分析小球A的运动情况．
练习册系列答案
阅读快车系列答案
相关题目
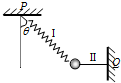如图，质量为m的小球与轻质弹簧Ⅰ和水平轻绳Ⅱ相连，Ⅰ、Ⅱ的另一端分别固定于P、Q，当剪断Ⅱ的瞬间，小球的加速度a应是（ ）
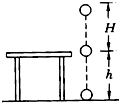如图，质量为m的小球，从离桌面高H处由静止下落，桌面离地面高为h，设桌面处物体重力势能为零，空气阻力不计，那么，小球落地时的机械能为（ ）
如图，质量为m的小球悬挂在长为L的细线下端，将它拉至与竖直方向成θ=60°的位置后自由释放．当小球摆至最低点时，恰好与水平面上原来静止的、质量为2m的木块相碰．不考虑空气阻力，重力加速度取g．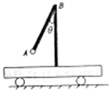
如图，质量为m的小球固定在细杆AB的一端，小车静止在水平面上，以下说法正确的是（ ）