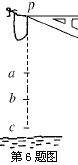题目内容
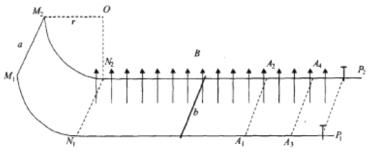
【题目】如图所示，两根平行光滑的金属导轨
由四分之一圆弧部分与水平部分构成，导轨末端固定两根绝缘柱，弧形部分半径r=0.8m、导轨间距L=lm， 导轨水平部分处于竖直向上的匀强磁场中，磁感应强度大小B=2T.两根完全相同的金属棒a、b分别垂直导轨静置于圆弧顶端M1、M2处和水平导轨中某位置，两金属棒质量均为m=lkg、电阻均为R=2
。金属棒a由静止释放，沿圆弧导轨滑入水平部分，此 后，金属棒b向右运动，在导轨末端与绝缘柱发生碰撞且无机械能损失，金属棒b接触绝缘柱之前两棒己匀速运动且未发生碰撞，金属棒b与绝缘柱发生碰撞后，在距绝缘柱 x1=0.5m的A1A2位置与金属棒a发生碰撞，碰后停在距绝缘柱x2=0.2m的A3A4位置， 整个运动过程中金属棒与导轨接触良好，导轨电阻不计，g取10m/s2。求：
（1）金属棒a刚滑入水平导轨时，受到的安培力大小；
（2）金属棒b与绝缘柱碰撞后到与金属棒a碰撞前的过程，整个回路产生的焦耳热；
（3）证明金属棒a、b的碰撞是否是弹性碰撞。
【答案】(1) 
(2) 
(3)碰撞不是弹性碰撞
【解析】
（1）对金属棒a下滑过程运用动能定理，求出金属棒a刚滑入水平导轨时的速度，根据法拉第电磁感应定律结合闭合欧姆定律以及安培力公式，联立即可求出安培力大小；
（2）利用动量守恒定律求出碰前两棒的共同速度，金属棒b与绝缘柱发生碰撞后等速率返回，再与金属棒a发生碰撞，对此过程再运用动量守恒定律，
（3）利用动量定理求出a、b棒碰撞后棒b的速度，再通过比较碰撞前碰撞后的总动能，即可判断出金属棒a、b的碰撞是否是弹性碰撞。
（1）金属棒a下滑过程运用动能定理可得：
，
金属棒a刚滑入水平导轨时，感应电动势：
，
回路电流：
，金属棒a受到的安培力：
；
（2）以金属棒a、b为系统，在碰到绝缘柱之前动量守恒：
，解得：
；
金属棒b与绝缘柱发生碰撞后等速率返回，以两金属棒为系统动量仍然守恒，但总动量为零，
；
即：时刻有
，两金属棒相向运动到相碰，位移大小相等均为0.5m；
电路中的瞬时感应电动势是两棒的叠加：
，
根据欧姆定律可得：
，金属棒b的安培力：
；
对金属棒b由动量定理：
，
其中：
，求得：
；
根据能量守恒可得整个回路产生的焦耳热：
；
（3）金属棒a、b碰后，金属棒b减速到零的过程，由动量定理：
，
由法拉第电磁感应定律：
电荷量：
；
求得：
，因为： 
，即：碰撞过程有动能损失，所以碰撞不是弹性碰撞。
应用题作业本系列答案
