题目内容
如图所示,竖直平面xoy内有三个宽度均为L首尾相接的电场区域ABFE、BCGF和CDHG.三个区域中分别存在方向+y、+y、+x的匀强电场,其场强大小比例为2:1:2.现有一带正电的物体以某一初速度从坐标为(0,L)的P点射入ABFE场区,初速度方向水平向右.物体恰从坐标为(2L,
)的Q点射入CDHG场区,已知物体在ABFE区域所受电场力和所受重力大小相等,重力加速度为g,物体可以视作质点,y轴竖直向上,区域内竖直方向电场足够大.求:
(1)物体进入ABFE区域时的衩速度大小;
(2)物体在ADHE区域运动的总时间;
(3)物体从DH边界射出位置的坐标.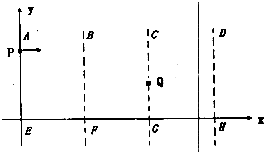
| L |
| 2 |
(1)物体进入ABFE区域时的衩速度大小;
(2)物体在ADHE区域运动的总时间;
(3)物体从DH边界射出位置的坐标.

设三个区域的电场强度大小依次为2E、E、2E,物体在三个区域运动的时间分别t1、t2、t3.
(1)在BCDF,对物体进行受力分析,由牛顿第二定律得
mg-qE=ma2,而2qE=mg
得a2=
在水平方向有:L=v0t
在竖直方向有:
=
a2
解得,v0=
,t2=
(2)在ABEF区域.对物体进行受力分析,在竖直方向有:2qE=mg
物体做匀速直线运动,v0=
,t1=t2=
在BCGF区域,物体做类平抛运动,v0=
,t2=
在Q点竖直方向速度vy=a2t2=
=v0,则Q点速度vQ=
=
,与水平方向夹角为45°
在CDHG区域 由于2qE=mg
对物体进行受力分析,F=
mg,与水平方向夹角为45°,与速度方向相同,物体做匀加速直线运动
水平方向L=v0t3+
a3
解得t3=
所以t=t1+t2+t3=
(3)物体在ABFE区域做匀速直线运动,在BCGF区域物体做类平抛运动,偏移量为
.在CDHG区域,沿与水平方向夹角为45°,物体做匀加速直线运动,竖直方向位移为L,则物体从DH边界射出位置的坐标为(3L,-
).
答:
(1)物体进入ABFE区域时的初速度大小v0=
;
(2)物体在ADHE区域运动的总时间为
;
(3)物体从DH边界射出位置的坐标为(3L,-
).
(1)在BCDF,对物体进行受力分析,由牛顿第二定律得
mg-qE=ma2,而2qE=mg
得a2=
| g |
| 2 |
在水平方向有:L=v0t
在竖直方向有:
| L |
| 2 |
| 1 |
| 2 |
| t | 22 |
解得,v0=
|
|
(2)在ABEF区域.对物体进行受力分析,在竖直方向有:2qE=mg
物体做匀速直线运动,v0=
|
|
在BCGF区域,物体做类平抛运动,v0=
|
|
在Q点竖直方向速度vy=a2t2=
|
|
| gL |
在CDHG区域 由于2qE=mg
对物体进行受力分析,F=
| 2 |
水平方向L=v0t3+
| 1 |
| 2 |
| t | 23 |
解得t3=
| ||
| 2 |
|
所以t=t1+t2+t3=
| ||
| 2 |
|
(3)物体在ABFE区域做匀速直线运动,在BCGF区域物体做类平抛运动,偏移量为
| L |
| 2 |
| L |
| 2 |
答:
(1)物体进入ABFE区域时的初速度大小v0=
|
(2)物体在ADHE区域运动的总时间为
| ||
| 2 |
|
(3)物体从DH边界射出位置的坐标为(3L,-
| L |
| 2 |

练习册系列答案
相关题目
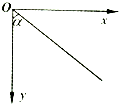 如图所示为竖直平面内的直角坐标系,其中x轴沿水平方向,y轴沿竖直方向.质量为m,电量为q的质点,在重力和恒定电场力F作用下,从坐标原点O由静止开始在竖直平面内沿与y正方向成α角(α>45°)斜向下做直线运动,重力加速度为g,则下列说法中正确的是( )
如图所示为竖直平面内的直角坐标系,其中x轴沿水平方向,y轴沿竖直方向.质量为m,电量为q的质点,在重力和恒定电场力F作用下,从坐标原点O由静止开始在竖直平面内沿与y正方向成α角(α>45°)斜向下做直线运动,重力加速度为g,则下列说法中正确的是( )| A、若F=mg sinα,则物体的机械能一定不变 | B、若F=mg tanα,则物体的机械能一定增大 | C、若F=mg tanα,则物体的机械能一定减小 | D、若F=mg tanα,则物体的电势能一定增大 |
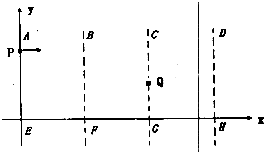 如图所示,竖直平面xoy内有三个宽度均为L首尾相接的电场区域ABFE、BCGF和CDHG.三个区域中分别存在方向+y、+y、+x的匀强电场,其场强大小比例为2:1:2.现有一带正电的物体以某一初速度从坐标为(0,L)的P点射入ABFE场区,初速度方向水平向右.物体恰从坐标为(2L,
如图所示,竖直平面xoy内有三个宽度均为L首尾相接的电场区域ABFE、BCGF和CDHG.三个区域中分别存在方向+y、+y、+x的匀强电场,其场强大小比例为2:1:2.现有一带正电的物体以某一初速度从坐标为(0,L)的P点射入ABFE场区,初速度方向水平向右.物体恰从坐标为(2L,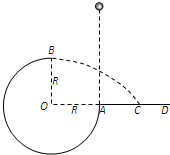 如图所示,竖直平面内的 3/4 圆弧形光滑轨道半径为 R,A 端与圆心 O 等高,AD 为水平面,B 点为光滑轨道的最高点且在O 的正上方,一个小球在 A 点正上方某处由静止释放,自由下落至 A 点进入圆轨道并知通过 B 点时受到轨道的弹力为mg(从A点进入圆轨道时无机械能损失),最后落到水平面 C 点处.求:
如图所示,竖直平面内的 3/4 圆弧形光滑轨道半径为 R,A 端与圆心 O 等高,AD 为水平面,B 点为光滑轨道的最高点且在O 的正上方,一个小球在 A 点正上方某处由静止释放,自由下落至 A 点进入圆轨道并知通过 B 点时受到轨道的弹力为mg(从A点进入圆轨道时无机械能损失),最后落到水平面 C 点处.求: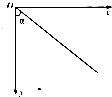 (2013?河南模拟)如图所示为竖直平面内的直角坐标系,其中x轴沿水平方向,y轴沿竖直方向.质量为m、带电荷量为q的小球,在重力和恒定电场力F作用下,在竖直平面内沿与y轴方向成α角(90°>α>45°)斜向下做直线运动,重力加速度为g,则下列说法正确的是( )
(2013?河南模拟)如图所示为竖直平面内的直角坐标系,其中x轴沿水平方向,y轴沿竖直方向.质量为m、带电荷量为q的小球,在重力和恒定电场力F作用下,在竖直平面内沿与y轴方向成α角(90°>α>45°)斜向下做直线运动,重力加速度为g,则下列说法正确的是( )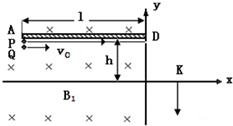 (2013?四川)如图所示,竖直平面(纸面)内有直角坐标系xOy,x轴沿水平方向.在x≤O的区域内存在方向垂直于纸面向里,磁感应强度大小为B1的匀强磁场.在第二象限紧贴y轴固定放置长为l、表面粗糙的不带电绝缘平板,平板平行于x轴且与x轴相距h.在第一象限内的某区域存在方向相互垂直的匀强磁场(磁感应强度大小为B2、方向垂直于纸面向外)和匀强电场(图中未画出).一质量为m、不带电的小球Q从平板下侧A点沿x轴正向抛出;另一质量也为m、带电量为q的小球P从A点紧贴平板沿x轴正向运动,变为匀速运动后从y轴上的D点进入电磁场区域做匀速圆周运动,经
(2013?四川)如图所示,竖直平面(纸面)内有直角坐标系xOy,x轴沿水平方向.在x≤O的区域内存在方向垂直于纸面向里,磁感应强度大小为B1的匀强磁场.在第二象限紧贴y轴固定放置长为l、表面粗糙的不带电绝缘平板,平板平行于x轴且与x轴相距h.在第一象限内的某区域存在方向相互垂直的匀强磁场(磁感应强度大小为B2、方向垂直于纸面向外)和匀强电场(图中未画出).一质量为m、不带电的小球Q从平板下侧A点沿x轴正向抛出;另一质量也为m、带电量为q的小球P从A点紧贴平板沿x轴正向运动,变为匀速运动后从y轴上的D点进入电磁场区域做匀速圆周运动,经