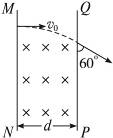
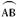题目内容
如图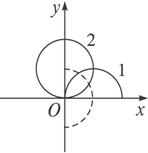
图
解析:带电粒子以某速度射入磁场后,在匀强磁场内做圆周运动时,其轨道半径取决于粒子速度的大小,但其圆轨道的圆心的位置却取决于粒子速度的方向.要确定在xOy平面内运动的粒子在磁场中可能到达的最大x和最大y值,就与圆周的圆心在何处有关.
质量为m、电荷量为q的正离子,从O点以速率v沿在xOy平面内的不同方向入射到匀强磁场区后做匀速圆周运动,正离子所受的洛伦兹力就是它做圆周运动所需的向心力,则为qvB=![]() ①
①
由式①求得正离子的轨道半径为R=![]() ②
②

图
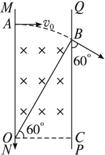
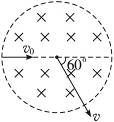
从放在原点O的离子源向x轴上方在xOy平面内各不同方向射出的质量为m、电荷量为q、速度为v的离子都在xOy平面内沿不同的圆周或圆弧轨道运动,这些离子运动轨道的半径都为R=![]() ,所有的圆周或圆弧都过O点,轨道的圆心到O点的距离也都等于R,圆心分布在图
,所有的圆周或圆弧都过O点,轨道的圆心到O点的距离也都等于R,圆心分布在图![]() .沿x轴负方向射入磁场的离子,其轨道的圆心在y轴上,此轨道即图中的圆轨道2.轨道与y轴的交点是离子在磁场内到达的最大y值,交点到原点O的距离为2R=
.沿x轴负方向射入磁场的离子,其轨道的圆心在y轴上,此轨道即图中的圆轨道2.轨道与y轴的交点是离子在磁场内到达的最大y值,交点到原点O的距离为2R=![]() .
.
答案: ![]()
![]()

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目