Question

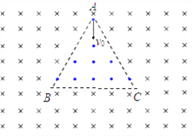
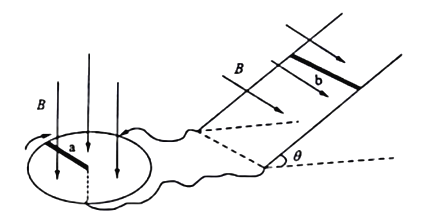
【题目】如图所示，半径为l的金属圆环水平放置，圆心处及圆环边缘通过导线分别与两条平行的倾斜金属轨道相连，圆环区域内分布着磁感应强度为B，方向竖直向下的匀强磁场，圆环上放置一金属棒a，一端在圆心处，另一端恰好在圆环上，可绕圆心转动，倾斜轨道部分处于垂直轨道平面向下的匀强磁场中，磁感应强度大小也为B，金属棒b放置在倾斜平行导轨上，其长度与导轨间距均为2l，当棒a绕圆心以角速度顺时针（俯视）匀速旋转时，棒b保持静止，已知棒b与轨道间的动摩擦因数为μ=0.5，可认为最大静摩擦力等于滑动摩擦力；棒b的质量为m，棒a、b的电阻分别为R、2R，其余电阻不计，斜面倾角为θ=37°sin37°=0.6，cos37°=0.8，重力加速度为g，求：

（1）金属棒b两端的电压；

（2）为保持b棒始终静止，棒a旋转的角速度大小的范围；

Answer 1

【答案】(1) (2)

【解析】（1）金属棒切割磁感线产生的感应电动势为①，②，

金属棒两端的电压③，联立①②③解得④；

（2）⑤，⑥，由①②⑤⑥解得，

为保持b棒始终静止，棒a旋转的角速度最小为，最大为，

，

，

解得