题目内容
4.如图所示,物体A放在足够长的木板B的右端,木板B静止于水平面.t=0时,电动机通过水平细绳以恒力F拉木板B,使它做初速度为零,加速度aB=1.0m/s2的匀加速直线运动.已知A的质量mA和B的质量mB均为2.0kg,A、B之间的动摩擦因数μ1=0.05,B与水平面之间的动摩擦因数μ2=0.1,最大静摩擦力与滑动摩擦力大小视为相等,重力加速度g取10m/s2.求:
(1)物体A刚运动时的加速度大小aA和方向;
(2)t=1.0s时,电动机的输出功率P;
(3)若t=1.0s时,将电动机的输出功率立即调整为P′=5W,并在以后的运动过程中始终保持这一功率不变,则再经过多长时间物体A与木板B的速度相等?
分析 (1)对A由牛顿第二定律可求得A刚运动时的加速度;
(2)对于木板B分析,由匀加速直线运动的规律可求得B点的速度;由功率公式可求得输入功率;
(3)对于木板B由功率公式可求得牵引力;再由牛顿第二定律可得出木板的加速度,从而分析木板的运动过程即可求解.
解答 解:(1)由牛顿第二定律可知:${a}_{A}=\frac{{μ}_{1}{m}_{A}g}{{m}_{A}}$=0.05×10=0.5m/s2,方向:水平向右;
(2)F-μ1mg-μ2(mA+mB)g=mBaB
代入数据解得:F=2×1+0.05×2×10+0.1×4×10=7N,
而由运动学公式可知:vB=aBt=1×1=1m/s;
由功率公式得:P=FvB=7×1=7W;
(3)物体A继续做加速运动,加速度仍为 aA=0.5m/s2
由 P′=F′vB
得 F′=$\frac{5}{1}$=5N
对于木板B,有:F″-μ1mg-μ2(mA+mB)g=mBa′B
解得:a′B=0;
即木板B做匀速直线运动.
由 aA(t+t′)=vB
可得 t′=$\frac{1}{0.5}$=1.0s
答:(1)物体A刚运动时的加速度大小为0.5m/s2,方向:水平向右;
(2)t=1.0s时,电动机的输出功率为7W;
(3)再经过1.0s物体A与木板B的速度相等.
点评 本题考查牛顿第二定律的应用及功率公式,对于牛顿第二定律的题目,要注意分析物体的运动过程,并正确确定研究对象,再由牛顿第二定律确定加速度,由运动学公式即可确定物体的速度及位移

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.从同一高度将三个质量相同的物体,以相等的速率同时抛出,一个水平抛出,一个竖直向上抛出,一个竖直向下抛出,从抛出到落地的运动过程中,以下说法正确的是( )
| A. | 重力对三个物体做功的平均功率有可能相同 | |
| B. | 落地时,三个物体的重力的瞬时功率有可能相同 | |
| C. | 重力对竖直上抛的物体做功最多,对竖直下抛的物体做功最少 | |
| D. | 三个物体落地时速率一定相同 |
12. 如图所示,导线框abcd与导线AB在同一平面内,直导线中通有恒定电流I,在线框由左向右匀速通过直导线的过程中,线框中的电流方向是( )
如图所示,导线框abcd与导线AB在同一平面内,直导线中通有恒定电流I,在线框由左向右匀速通过直导线的过程中,线框中的电流方向是( )
 如图所示,导线框abcd与导线AB在同一平面内,直导线中通有恒定电流I,在线框由左向右匀速通过直导线的过程中,线框中的电流方向是( )
如图所示,导线框abcd与导线AB在同一平面内,直导线中通有恒定电流I,在线框由左向右匀速通过直导线的过程中,线框中的电流方向是( )| A. | 先abcda,再adcba,后abcda | B. | 先abcda,再adcba | ||
| C. | 始终adcba | D. | 先adcba,再abcda,后adcba |
19. 如图所示,固定斜面倾角为θ,整个斜面分为AB、BC两段,且AB=2BC.小物块P(可视为质点)与AB、BC两段斜面之间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放,恰好能滑动到C点而停下,已知θ=37°(sin37°=0.6,cos37°=0.8)则下列说法正确的是( )
如图所示,固定斜面倾角为θ,整个斜面分为AB、BC两段,且AB=2BC.小物块P(可视为质点)与AB、BC两段斜面之间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放,恰好能滑动到C点而停下,已知θ=37°(sin37°=0.6,cos37°=0.8)则下列说法正确的是( )
 如图所示,固定斜面倾角为θ,整个斜面分为AB、BC两段,且AB=2BC.小物块P(可视为质点)与AB、BC两段斜面之间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放,恰好能滑动到C点而停下,已知θ=37°(sin37°=0.6,cos37°=0.8)则下列说法正确的是( )
如图所示,固定斜面倾角为θ,整个斜面分为AB、BC两段,且AB=2BC.小物块P(可视为质点)与AB、BC两段斜面之间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放,恰好能滑动到C点而停下,已知θ=37°(sin37°=0.6,cos37°=0.8)则下列说法正确的是( )| A. | 物块在AB间运动的时间是BC间运动时间的2倍 | |
| B. | 物块在AB间运动的平均速度与BC间运动平均速度相等 | |
| C. | 物块在AB间运动的加速度大小是在BC间运动加速度大小的$\frac{1}{2}$ | |
| D. | μ2=2μ1 |
9.以下说法中正确的是( )
| A. | 力是产生加速度的原因 | |
| B. | 力是维持物体运动的原因 | |
| C. | 速度越大的物体越难让它停止运动,故速度越大,惯性越大 | |
| D. | 物体在地球上的惯性比在月球上的大 |
16.如图所示,螺线管匝数n=1000匝,横截面积S=10cm2,螺线管导线电阻r=1Ω,电阻R=4Ω,磁感应强度B随时间变化的图象如图所示(以向右为正方向),下列说法正确的是( )


| A. | 通过电阻R的电流是交变电流 | B. | 感应电流的大小保持不变 | ||
| C. | 电阻R两端的电压为6V | D. | C点的电势为6V |
13.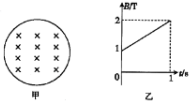 如图甲所示,面积为S=1m2的导体圆环内通有垂直于圆平面向里的磁场,磁场的磁感应强度B随时间t变化的关系如图乙所所示(B取向里方向为正),以下说法中正确的是( )
如图甲所示,面积为S=1m2的导体圆环内通有垂直于圆平面向里的磁场,磁场的磁感应强度B随时间t变化的关系如图乙所所示(B取向里方向为正),以下说法中正确的是( )
 如图甲所示,面积为S=1m2的导体圆环内通有垂直于圆平面向里的磁场,磁场的磁感应强度B随时间t变化的关系如图乙所所示(B取向里方向为正),以下说法中正确的是( )
如图甲所示,面积为S=1m2的导体圆环内通有垂直于圆平面向里的磁场,磁场的磁感应强度B随时间t变化的关系如图乙所所示(B取向里方向为正),以下说法中正确的是( )| A. | 环中产生顺时针方向的感应电流 | B. | 环中产生逆时针方向的感应电流 | ||
| C. | 环中产生的感应电动势大小为2V | D. | 环中产生的感应电动势大小为1V |
14.下列说法正确的是( )
| A. | 牛顿不仅提出了万有引力定律而且测量出了引力常量 | |
| B. | 库仑在发现电荷间相互作用力规律之前,首先找到了定量测定电荷量的方法 | |
| C. | 库仑利用库仑扭秤巧妙地实现了他对电荷间相互作用力规律的研究 | |
| D. | 在国际单位中,力学的基本单位是米、牛顿、秒 |