题目内容
汽车甲沿着平直的公路以速度v做匀速直线运动,当它路过某处的同时,该处有一汽车乙开始做初速度为零的匀加速运动去追赶甲,根据上述已知条件,下列说法正确的是( )
| A.可求出乙车追上甲车时,乙车的速度。 |
| B.可求出乙车追上甲车时,乙车所走过的路程。 |
| C.可求出乙车从开始到追上甲车时所用的时间。 |
| D.可求出乙车从开始到追上甲车之前,甲乙相距最远时乙车的速度。 |
AD
题中涉及到2个相关物体运动问题,分析出2个物体各作什么运动,并尽力找到两者相关的物理条件是解决这类问题的关键,通常可以从位移关系、速度关系或者时间关系等方面去分析。
解析:根据题意,从汽车乙开始追赶汽车甲直到追上,两者运动距离相等,即s甲=
=s乙=s,经历时间t甲=t乙=t.
那么,根据匀速直线运动公式对甲应有: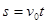
根据匀加速直线运动公式对乙有: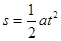 ,及
,及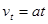
由前2式相除可得at=2v0,代入后式得vt=2v0,这就说明根据已知条件可求出乙车追上甲车时乙车的速度应为2v0。因a不知,无法求出路程和时间,如果我们采取作v-t图线的方法,则上述结论就比较容易通过图线看出。图中当乙车追上甲车时,路程应相等,即从图中图线上看面积s甲和s乙,显然三角形高vt等于长方形高v0的2倍,由于加速度a未知,乙图斜率不定,a越小,t越大,s也越大,也就是追赶时间和路程就越大
解析:根据题意,从汽车乙开始追赶汽车甲直到追上,两者运动距离相等,即s甲=
=s乙=s,经历时间t甲=t乙=t.
那么,根据匀速直线运动公式对甲应有:
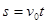
根据匀加速直线运动公式对乙有:
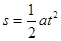 ,及
,及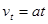
由前2式相除可得at=2v0,代入后式得vt=2v0,这就说明根据已知条件可求出乙车追上甲车时乙车的速度应为2v0。因a不知,无法求出路程和时间,如果我们采取作v-t图线的方法,则上述结论就比较容易通过图线看出。图中当乙车追上甲车时,路程应相等,即从图中图线上看面积s甲和s乙,显然三角形高vt等于长方形高v0的2倍,由于加速度a未知,乙图斜率不定,a越小,t越大,s也越大,也就是追赶时间和路程就越大

练习册系列答案
相关题目
