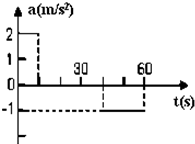
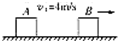题目内容
如图所示,A物体由静止出发,以加速度5m/s2追赶正前方5m的B物体,B物体一直以速度5m/s作匀速直线运动,A、B可看作质点,求:
(1)A追上B前两者相距的最大距离为多少?
(2)A经历多少时间追上B?
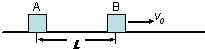
(1)A追上B前两者相距的最大距离为多少?
(2)A经历多少时间追上B?

(1)当A、B速度相等时,两物体的距离最大,此时vA=vB
设经过时间t,速度相等,则
5t=5
解得:t=1s
则sA=
at2=
×5×1=2.5m
sB=vBt=1×5=5m
所以A、相距△s=sB+L-sA=5+5-2.5=7.5m
(2)设经过时间t′,AB相遇,则
at′2=L+vBt′
即
×5t′2=5+5t′
解得:t′=2+
s
答:(1)A追上B前两者相距的最大距离为7.5m;
(2)A经历2+
s追上B.
设经过时间t,速度相等,则
5t=5
解得:t=1s
则sA=
| 1 |
| 2 |
| 1 |
| 2 |
sB=vBt=1×5=5m
所以A、相距△s=sB+L-sA=5+5-2.5=7.5m
(2)设经过时间t′,AB相遇,则
| 1 |
| 2 |
即
| 1 |
| 2 |
解得:t′=2+
| 3 |
答:(1)A追上B前两者相距的最大距离为7.5m;
(2)A经历2+
| 3 |

练习册系列答案
相关题目