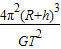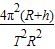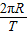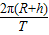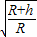题目内容
我国于2004年启动“嫦娥绕月工程”,2007年10月24日发射了绕月飞行的嫦娥一号探月卫星.卫星在成功发射后,将在地球轨道上经历3次调相轨道变轨,已于10月31日进入地月转移轨道,开始奔向月球.在11月5日进入月球轨道后,经历3次轨道调整,进入工作轨道.此后,卫星计划在此轨道上将继续工作1年时间,对月球进行科学探测.已知卫星到达工作运行轨道后,关闭发动机绕月做匀速圆周运动,测得卫星距离月球表面的高度h,运动周期为T,已知月球半径R,万有引力常量为G.由此可知( )
分析:卫星绕月球做匀速圆周运动,由万有引力提供向心力,根据牛顿第二定律列式可求得月球的质量.在月球表面,物体的重力等于月球的万有引力,列式得到月球表面的重力加速度.卫星的轨道半径为R+h,由圆周运动规律可得到其线速度.当卫星绕月球表面运行时其速度等于第一宇宙速度.
解答:解:A、卫星绕月球做匀速圆周运动,由万有引力提供向心力,则有G
=m
(R+h)
则得月球的质量为M=
.故A正确.
B、在月球表面,物体的重力等于月球的万有引力,则有m′g=G
得月球表面的重力加速度g=
=
=
.故B错误.
C、卫星的轨道半径为R+h,线速度为v=
.故C错误.
D、当卫星绕月球表面运行时,有G
=m
则得月球的第一宇宙速度为
.故D正确.
故选AD
| Mm |
| (R+h)2 |
| 4π2 |
| T2 |
则得月球的质量为M=
| 4π2(R+h)3 |
| GT2 |
B、在月球表面,物体的重力等于月球的万有引力,则有m′g=G
| Mm′ |
| R2 |
得月球表面的重力加速度g=
| GM |
| R2 |
G?
| ||
| R2 |
| 4π2(R+h)3 |
| T2R2 |
C、卫星的轨道半径为R+h,线速度为v=
| 2π(R+h) |
| T |
D、当卫星绕月球表面运行时,有G
| Mm |
| R2 |
| ||
| R |
则得月球的第一宇宙速度为
| 2π(R+h) |
| T |
|
故选AD
点评:对于卫星类型,关键分析向心力的来源,运用万有引力定律、牛顿第二定律和圆周运动的规律列式进行分析即可.

练习册系列答案
相关题目