题目内容
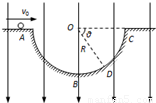
在光滑绝缘的水平面上有半圆柱形的凹槽ABC，截面半径为R=0.4m．空间有竖直向下的匀强电场，一个质量m=0.02kg，带电量q=+1.0×10-3 C的小球（可视为质点）以初速度v=4m/s从A点水平飞入凹槽，恰好撞在D点，D与O的连线与水平方向夹角为θ=53°，已知重力加速度为g=10m/s2，sin 53°=0.8，cos 53°=0.6，试求：（1）小球从A飞到D所用的时间t；
（2）电场强度E的大小；
（3）A、D两点间的电势差UAD．
【答案】分析：小球水平方向不受力，做匀速直线运动，竖直方向做匀加速直线运动，根据运动学知识和牛顿第二定律即可求解．
解答：解：（1）水平方向上，小球做匀速直线运动
Vt=R+Rcosθ
得t=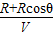
=
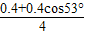=0.16s
（2）在竖直方向上，小球做匀加速直线运动，
Rsinθ=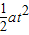
由牛顿第二定律知
mg+qE=ma
代入数据得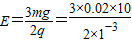
=300V/m
（3）由匀强电场中电势差与电场强度的关系，有
UAD=ERsinθ=300×0.4sin53°=96V
答：（1）小球从A飞到D所用的时间为0.16s；
（2）电场强度E的大小为300V/m；
（3）A、D两点间的电势差为96V．
点评：把小球的运动看做类平抛运动，应用平抛运动的知识可解决此类问题．
解答：解：（1）水平方向上，小球做匀速直线运动
Vt=R+Rcosθ
得t=
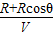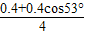==0.16s （2）在竖直方向上，小球做匀加速直线运动，
Rsinθ=
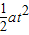
由牛顿第二定律知
mg+qE=ma
代入数据得
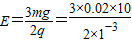=300V/m （3）由匀强电场中电势差与电场强度的关系，有
UAD=ERsinθ=300×0.4sin53°=96V
答：（1）小球从A飞到D所用的时间为0.16s；
（2）电场强度E的大小为300V/m；
（3）A、D两点间的电势差为96V．
点评：把小球的运动看做类平抛运动，应用平抛运动的知识可解决此类问题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在光滑绝缘的水平面上，用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B．A球的带电量为+2q，B球的带电量为-3q，组成一带电系统，如图所示．虚线MP为AB两球连线的垂直平分线，虚线NQ与MP平行且相距4L．最初A和B分别静止于虚线MP的两侧，距MP的距离均为L，且A球距虚线NQ的距离为3L．若视小球为质点，不计轻杆的质量，在虚线MP，NQ间加上水平向右的匀强电场E后，则带电系统从开始运动到速度第一次为零B球电势能的变化量（ ）
如图所示，在光滑绝缘的水平面上有一个用一根均匀导体围成的正方形线框abcd，其边长为L，总电阻为R，放在磁感应强度为B．方向竖直向下的匀强磁场的左边，图中虚线MN为磁场的左边界．线框在恒力作用下向右运动，其中ab边保持与MN平行．当线框以速度v0进入磁场区域时，它恰好做匀速运动，求：
如图所示，在光滑绝缘的水平面上固定两个等量负点电荷A和B，O点为AB连线的中点，C、D为AB连线上关于0点对称的两个点，且CO=OD=L．一带正电的可视为点电荷的小球以初速度v．从C点运动到D点．设O点的电势?0=0，取C点为坐标原点，向右为x轴的正方向，在下列中关于小球的电势能EP、小球的动能EK、电势?、电场强度E与小球运动的位移x变化的图象，可能正确的是（ ）
如图所示，在光滑绝缘的水平面上，有一静止在A点质量为m=1×10-3kg、带正电的小球，现加一水平方向的匀强电场使小球由A点运动到B点，静电力做功为W=0.2J，已知A、B两点间距离为L=0.1m，电势差为UAB=20V，
在光滑绝缘的水平面上有半圆柱形的凹槽ABC，截面半径为R=0.4m．空间有竖直向下的匀强电场，一个质量m=0.02kg，带电量q=+l．0×l0-3 C的小球（可视为质点）以初速度v0=4m/s从A点水平飞人凹槽，恰好撞在D点，D与O的连线与水平方向夹角为θ=53°，重力加速度取g=10m/s2，sin 53°=0.8．cos 53°=0.6，试求：