题目内容
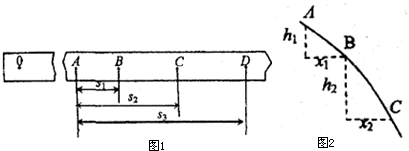
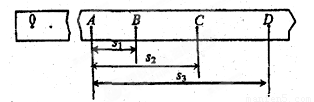
某同学研究小车在斜面上的运动,用打点计时器记录了小车做匀变速直线运动的位移,得到一段纸带如图所示。在纸带上选取几个相邻计数点A、B、C、D,相邻计数点间的时间间隔均为T,B、C和D各点到A的距离为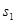 、
、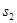 和
和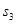 。由此可算出小车运动的加速度大小
。由此可算出小车运动的加速度大小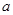 =____________________,打点计时器在打C点时,小车的速度大小
=____________________,打点计时器在打C点时,小车的速度大小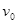 =_______。 (用已知的物理量符号表示)
=_______。 (用已知的物理量符号表示)
【答案】
a=(s3-2s2+s1)/T2 v0=(s3-s1)/2T
【解析】
试题分析:据题意,利用逐差法可得:a=(sCD-sBC)/T2,而sCD=s3-s2,sBC=s2-s1,所以可以求得加速度为a=(s3-2s2+s1)/T2;C点的瞬时速度等于BD段的平均速度,即vc=(s3-s1)/2T。
考点:本题考查对打点计时器测量物体加速度和速度的理解。

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目

 某同学研究小车在斜面上的运动,用打点计时器记录了小车做匀变速直线运动的位移,得到一段纸带如图所示.在纸带上选取几个相邻计数点A、B、C、D,相邻计数点间的时间间隔均为T,B、C和D各点到A的距离为s1、s2和s3.由此可算出小车运动的加速度大小a=
某同学研究小车在斜面上的运动,用打点计时器记录了小车做匀变速直线运动的位移,得到一段纸带如图所示.在纸带上选取几个相邻计数点A、B、C、D,相邻计数点间的时间间隔均为T,B、C和D各点到A的距离为s1、s2和s3.由此可算出小车运动的加速度大小a=