题目内容
【题目】一个倾角为θ=37°的斜面固定在水平面上,一个质量为m=2.0kg的小物块(可视为质点)以v0=5.0m/s的初速度由底端沿斜面上滑,小物块与斜面的动摩擦因数μ=0.5.若斜面足够长,已知sin37°=0.6,cos37°=0.8,g取10m/s2,求:

(1)小物块沿斜面上滑时的加速度大小;
(2)小物块上滑的最大距离;
(3)小物块返回斜面底端时的速度大小.(可用根式表示)
【答案】(1)10m/s2(2)![]() (3)
(3)![]() m/s
m/s
【解析】(1)小物块在斜面上的受力情况如右图所示,
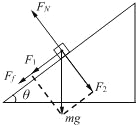
根据牛顿第二定律有
FN=mgcosθ①
mgsinθ+Ff=ma②
又 Ff=μFN③
由①②③式得a=gsinθ+μgcosθ=10m/s2④
(2)小物块沿斜面上滑做匀减速运动,到达最高点时速度v=0,则有![]() ⑤
⑤
得![]() ⑥
⑥
(3)小物块在斜面上的受力情况如图所示
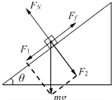
根据牛顿第二定律有FN=F2⑦
F1﹣Ff=ma'⑧
由③⑦⑧式得a'=gsinθ﹣μgcosθ=2m/s2⑨
因为![]() ⑩
⑩
所以![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目