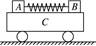
题目内容
如图所示,在光滑水平地面上,有一质量m1= 4.0kg的平板小车,小车的右端有一固定的竖直挡板,挡板上固定一轻质细弹簧。位于小车上A点处质量m2=1.0kg的木块(可视为质点)与弹簧的左端相接触但不连接,此时弹簧与木块间无相互作用力。木块与A点左侧的车面之间的动摩擦因数μ= 0.40,木块与A点右侧的车面之间的摩擦可忽略不计。现小车与木块一起以v0= 2.0m/s的初速度向右运动,小车将与其右侧的竖直墙壁发生碰撞,已知碰撞时间极短,碰撞后小车以v 1= 1.0m/s的速度反向弹回,已知重力加速度g取10m/s2,弹簧始终处于弹性限度内。求:
(1)小车撞墙后弹簧的最大弹性势能;
(2)要使木块最终不从小车上滑落,则车面A点左侧粗糙部分的长度应满足什么条件?
(1)小车撞墙后弹簧的最大弹性势能;
(2)要使木块最终不从小车上滑落,则车面A点左侧粗糙部分的长度应满足什么条件?

(1)EP=3.6J
(2)车面A点左侧粗糙部分的长度应大于0.90m。
(2)车面A点左侧粗糙部分的长度应大于0.90m。
(1)小车与墙壁碰撞后向左运动,木块与小车间发生相对运动将弹簧压缩至最短时,二者速度相等,此时弹簧的弹性势能最大,此过程中,二者组成的系统动量守恒,设弹簧压缩至最短时,小车和木块的速度大小为v,根据动量守恒定律有:
m1v1-m2v0=(m1+m2)v, ①
解得 v=0.40m/s。 ②
设最大的弹性势能为EP,根据机械能守恒定律可得
EP=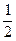 m1v12+
m1v12+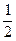 m2v02-
m2v02-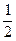 (m1+m2)v2, ③
(m1+m2)v2, ③
由②③得EP=3.6J。 ④
(2)根据题意,木块被弹簧弹出后滑到A点左侧某处与小车具有相同的速度v’时,木块将不会从小车上滑落, 此过程中,二者组成的系统动量守恒,故有v’ =v=0.40m/s,⑤
木块在A点右侧运动过程中,系统的机械能守恒,而在A点左侧相对滑动过程中将克服摩擦阻力做功,设此过程中滑行的最大相对位移为L,根据功能关系有
μm2gL=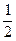 m1v12+
m1v12+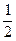 m2v02-
m2v02-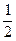 (m1+m2)v’2, ⑥
(m1+m2)v’2, ⑥
解得L=0.90m, ⑦
即车面A点左侧粗糙部分的长度应大于0.90m。
m1v1-m2v0=(m1+m2)v, ①
解得 v=0.40m/s。 ②
设最大的弹性势能为EP,根据机械能守恒定律可得
EP=
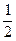 m1v12+
m1v12+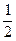 m2v02-
m2v02-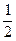 (m1+m2)v2, ③
(m1+m2)v2, ③由②③得EP=3.6J。 ④
(2)根据题意,木块被弹簧弹出后滑到A点左侧某处与小车具有相同的速度v’时,木块将不会从小车上滑落, 此过程中,二者组成的系统动量守恒,故有v’ =v=0.40m/s,⑤
木块在A点右侧运动过程中,系统的机械能守恒,而在A点左侧相对滑动过程中将克服摩擦阻力做功,设此过程中滑行的最大相对位移为L,根据功能关系有
μm2gL=
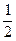 m1v12+
m1v12+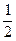 m2v02-
m2v02-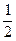 (m1+m2)v’2, ⑥
(m1+m2)v’2, ⑥解得L=0.90m, ⑦
即车面A点左侧粗糙部分的长度应大于0.90m。

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目

 )
)
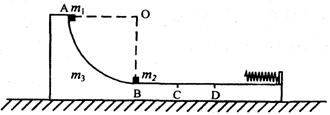
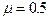 ,当木块运动到最左端A点时,一颗质量为m=20g的子弹,以v0=300m/s的水平向右的速度,正对射入木块并穿出,穿出速度v=50m/s,设子弹射穿木块的时间极短,(g取10m/s2)求:
,当木块运动到最左端A点时,一颗质量为m=20g的子弹,以v0=300m/s的水平向右的速度,正对射入木块并穿出,穿出速度v=50m/s,设子弹射穿木块的时间极短,(g取10m/s2)求: