题目内容
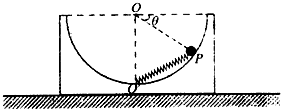如图所示，将一劲度系数为k的轻弹簧一端固定在内壁光滑、半径为R的半球形容器底部处O'（O为球心），弹簧另一端与质量为m的小球相连，小球静止于P点．已知容器与水平面间的动摩擦因数为μ，OP与水平方向的夹角为0=30°．下列说法正确的是
- A.水平面对容器有向右的摩擦力
- B.轻弹簧对小球的作用力大小为
mg - C.容器对小球的作用力大小为mg
- D.弹簧原长为
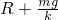
CD
分析：对容器和小球整体研究，分析受力可求得半球形容器受到的摩擦力．对小球进行受力分析可知，小球受重力、支持力及弹簧的弹力而处于静止，由共点力的平衡条件可求得小球受到的轻弹簧的弹力及小球受到的支持力，由胡克定律求出弹簧的压缩量，即可求得原长．
解答：A、以容器和小球整体为研究对象，分析受力可知：竖直方向有：总重力、地面的支持力，水平方向地面对半球形容器没有摩擦力．故A错误．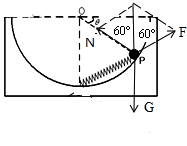
B、C对小球受力分析：重力G、弹簧的弹力F和容器的支持力N，如图所示，由平衡条件和几何关系可知，N=F=mg，故B错误；C正确；
D、由胡克定律得：弹簧的压缩量为x=
=
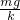，则弹簧的原长为R+x=R+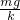，故D正确．
故选CD
点评：共点力平衡问题重点在于正确选择研究对象，本题运用隔离法和整体法两种方法进行受力分析得出结论．
分析：对容器和小球整体研究，分析受力可求得半球形容器受到的摩擦力．对小球进行受力分析可知，小球受重力、支持力及弹簧的弹力而处于静止，由共点力的平衡条件可求得小球受到的轻弹簧的弹力及小球受到的支持力，由胡克定律求出弹簧的压缩量，即可求得原长．
解答：A、以容器和小球整体为研究对象，分析受力可知：竖直方向有：总重力、地面的支持力，水平方向地面对半球形容器没有摩擦力．故A错误．
B、C对小球受力分析：重力G、弹簧的弹力F和容器的支持力N，如图所示，由平衡条件和几何关系可知，N=F=mg，故B错误；C正确；
D、由胡克定律得：弹簧的压缩量为x=
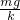=，则弹簧的原长为R+x=R+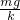，故D正确．故选CD
点评：共点力平衡问题重点在于正确选择研究对象，本题运用隔离法和整体法两种方法进行受力分析得出结论．
练习册系列答案
阅读快车系列答案
相关题目
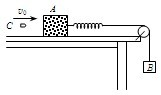如图所示，劲度系数为k的轻质水平弹簧的左端固定在质量为mA=4m的物块A上，右端系一不可伸长的轻质细线，细线绕过轻质光滑的定滑轮后与质量为mB=2m的小物块B相连．物块A放在足够长的水平桌面上，它与桌面间的摩擦因数μ，且知物块A与桌面的最大静摩擦力正好等于滑动摩擦力．滑轮以左的细线始终处于水平，整个系统当初处于静止状态．某时刻，一颗质量等于m的子弹以初速度v0水平击中物块A，并留在其中，物块A向前滑行一小段距离s而停下，此后将不再滑动．试求：
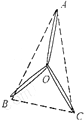
（2011?天门模拟）如图所示，在倾角为30°的光滑斜面上，一劲度系数为k的轻质弹簧一端固定在固定挡板C上，另一端连接一质量为m的物体A，一轻细绳通过定滑轮，一端系在物体A上，另一端有一细绳套，细绳与斜面平行，物体A处于静止状态．现在细绳套上轻轻挂上一个质量也为m的物体B，A将在斜面上做简谐运动．试求：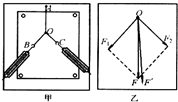
在“探究力的平行四边形定则”的实验中，用图钉把橡皮条的一端固定在板上的A点，在橡皮条的另一端拴上两条细绳，细绳另一端系着绳套B、C（用来连接弹簧测力计）．其中A为固定橡皮筋的图钉，O为橡皮筋与细绳的结点，OB和OC为细绳．图乙是在白纸上根据实验结果画出的图．
