题目内容
(2011?泰州一模)一根弹性细绳劲度系数为K,将其一端固定,另一端穿过一光滑小孔O系住一质量为m的滑块,滑块放在水平地面上.当细绳竖直时,小孔O到悬点的距离恰为弹性细绳原长,小孔O到正下方水平地面上P点的距离为h(h<
滑块与水平地面间的动摩擦因数为u,设最大静摩擦力等于滑动摩擦力,弹性细绳始终在其弹性限度内.
求:
(1)当滑块置于水平面能保持静止时,滑块到P点的最远距离;
(2)如果滑块从P点向右匀速运动,就需给滑块一水平向右的力F,力F与时间t的关系为如图所示的直线,已知图线的斜率为b.根据图线求滑块匀速运动的速度;
(3)若在上述匀速运动的过程中,滑块从P点向右运动了S的距离,求拉力F所做的功.
| mg | k |

求:
(1)当滑块置于水平面能保持静止时,滑块到P点的最远距离;
(2)如果滑块从P点向右匀速运动,就需给滑块一水平向右的力F,力F与时间t的关系为如图所示的直线,已知图线的斜率为b.根据图线求滑块匀速运动的速度;
(3)若在上述匀速运动的过程中,滑块从P点向右运动了S的距离,求拉力F所做的功.
分析:(1)当滑块置于水平面能保持静止离P点最远时,静摩擦力恰好达到最大值,根据平衡条件和胡克定律列式求出滑块到P点的最远距离.
(2)根据平衡条件和位移公式得到力F与时间t的关系图象,由数学知识求出滑块匀速运动的速度.
(3)由平衡条件得到力F与位移S的图象,图线所围成的面积即为外力F所做的功,由几何知识求解拉力F所做的功.
(2)根据平衡条件和位移公式得到力F与时间t的关系图象,由数学知识求出滑块匀速运动的速度.
(3)由平衡条件得到力F与位移S的图象,图线所围成的面积即为外力F所做的功,由几何知识求解拉力F所做的功.
解答: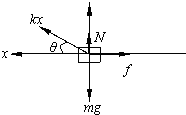 解:(1)设滑块离P点最远时,弹性绳伸长x,弹性绳与水平面夹角为θ,滑块到P点的最远距离为L,受力如图所示,
解:(1)设滑块离P点最远时,弹性绳伸长x,弹性绳与水平面夹角为θ,滑块到P点的最远距离为L,受力如图所示,
kxcosθ=μN…①
N+kxsinθ=mg…②
又h=xsinθ…③
L=xcosθ…④
由①②③④解得:
L=
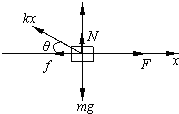 (2)滑块向右匀速运动时,受力如图所示,
(2)滑块向右匀速运动时,受力如图所示,
F=kxcosθ+μN…⑤
N+kxsinθ=mg…⑥
又vt=xcosθ…⑦
由③⑤⑥⑦解得:
F=kvt+μ(mg-kh)
 结合F与时间t的关系图线,可得:
结合F与时间t的关系图线,可得:
kv=b
∴v=
(3)设滑块匀速移动的位移为S,有:
s=vt…⑧
由⑤⑥⑧得:F=ks+μ(mg-kh)
由此作出F-S的关系图线,则图线所围成的面积即为外力F所做的功:
W=
答:
(1)当滑块置于水平面能保持静止时,滑块到P点的最远距离是
;
(2)根据图线求滑块匀速运动的速度是
;
(3)在上述匀速运动的过程中,滑块从P点向右运动了S的距离,拉力F所做的功是
.
 解:(1)设滑块离P点最远时,弹性绳伸长x,弹性绳与水平面夹角为θ,滑块到P点的最远距离为L,受力如图所示,
解:(1)设滑块离P点最远时,弹性绳伸长x,弹性绳与水平面夹角为θ,滑块到P点的最远距离为L,受力如图所示,kxcosθ=μN…①
N+kxsinθ=mg…②
又h=xsinθ…③
L=xcosθ…④
由①②③④解得:
L=
| μ(mg-kh) |
| k |
 (2)滑块向右匀速运动时,受力如图所示,
(2)滑块向右匀速运动时,受力如图所示,F=kxcosθ+μN…⑤
N+kxsinθ=mg…⑥
又vt=xcosθ…⑦
由③⑤⑥⑦解得:
F=kvt+μ(mg-kh)
 结合F与时间t的关系图线,可得:
结合F与时间t的关系图线,可得:kv=b
∴v=
| b |
| k |
(3)设滑块匀速移动的位移为S,有:
s=vt…⑧
由⑤⑥⑧得:F=ks+μ(mg-kh)
由此作出F-S的关系图线,则图线所围成的面积即为外力F所做的功:
W=
| ks2+2μ(mg-kh)s |
| 2 |
答:
(1)当滑块置于水平面能保持静止时,滑块到P点的最远距离是
| μ(mg-kh) |
| k |
(2)根据图线求滑块匀速运动的速度是
| b |
| k |
(3)在上述匀速运动的过程中,滑块从P点向右运动了S的距离,拉力F所做的功是
| ks2+2μ(mg-kh)s |
| 2 |
点评:本题的难点是根据平衡条件和位移公式得到F与t解析式及F与s的表达式,作出图象,抓住图象的数学意义进行分析.第3问题,也可以根据能量转化和守恒定律这样列方程求解:
W=
k(
)2-
kh2+μ(mg-kh)s=
ks2+μ(mg-kh)s
W=
| 1 |
| 2 |
| s2+h2 |
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 (2011?泰州一模)点电荷A、B是带电量为Q的正电荷,C、D是带电量为Q的负电荷,它们处在一个矩形的四个顶点上.它们产生静电场的等势面如图中虚线所示,在电场中对称地有一个正方形路径abcd(与ABCD共面),如图中实线所示,O为正方形与矩形的中心,则( )
(2011?泰州一模)点电荷A、B是带电量为Q的正电荷,C、D是带电量为Q的负电荷,它们处在一个矩形的四个顶点上.它们产生静电场的等势面如图中虚线所示,在电场中对称地有一个正方形路径abcd(与ABCD共面),如图中实线所示,O为正方形与矩形的中心,则( ) 图所示.开始时使弹簧伸长,放开物块后物块沿斜面向上运动,然后上滑到最高点,在此过程中,M保持静止状态,则地面对M的摩擦力( )
图所示.开始时使弹簧伸长,放开物块后物块沿斜面向上运动,然后上滑到最高点,在此过程中,M保持静止状态,则地面对M的摩擦力( ) (2011?泰州一模)如图所示,用三条细线悬挂的金属圆环,金属环粗细均匀、单位长度的质量为2.5g,三条细线呈对称分布,稳定时金属环面水平,在金属环正下方放有一个圆柱形磁铁,磁铁的中轴线OO′垂直于金属环面且通过其圆心O,测得金属环所在处磁感应强度大小为0.5T,与竖直方向成30°角.现在要使金属环各部分所受安培力的合力竖直向上且恰好等于其自身的重力,则在金属环中通过的电流大小至少为( )(取g=10m/s2)
(2011?泰州一模)如图所示,用三条细线悬挂的金属圆环,金属环粗细均匀、单位长度的质量为2.5g,三条细线呈对称分布,稳定时金属环面水平,在金属环正下方放有一个圆柱形磁铁,磁铁的中轴线OO′垂直于金属环面且通过其圆心O,测得金属环所在处磁感应强度大小为0.5T,与竖直方向成30°角.现在要使金属环各部分所受安培力的合力竖直向上且恰好等于其自身的重力,则在金属环中通过的电流大小至少为( )(取g=10m/s2) (2011?泰州一模)如图所示,Dl、D2规格相同的两个小灯泡,L是带有铁芯的电阻忽略不计的电感线圈,下列说法正确的是( )
(2011?泰州一模)如图所示,Dl、D2规格相同的两个小灯泡,L是带有铁芯的电阻忽略不计的电感线圈,下列说法正确的是( )