题目内容
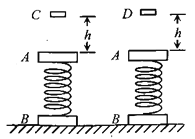
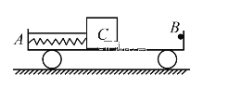
【题目】如图所示,小车AB静止于水平面上,A端固定一个轻质弹簧,B端粘有橡皮泥。小车AB质量为 M,质量为m的木块C放在小车上,CB距离为L用细线将木块连接于小车的A端并使弹簧压缩。开始时小车AB与木块C都处于静止状态,现烧断细线,弹簧被释放,使木块离开弹簧向B端滑去,并跟B端橡皮泥粘在一起。所有摩擦均不计,对整个过程,以下说法正确的是
A. 整个系统机械能守恒
B. 整个系统机械能不守恒,动量也不守恒
C. 当木块的速度最大时,小车的速度也最大
D. 最终整个系统匀速运动
【答案】C
【解析】
弹簧被释放过程系统机械能守恒,而木块C跟B端橡皮泥粘在一起的过程是非弹性碰撞,机械能有损失,所以整个系统机械能不守恒。故A错误。整个系统受到的合外力保持为零,动量守恒。故B错误。设弹簧释放后,木块C速度大小为v,小车速度为V,取向右为正方向,由动量守恒定律得:mv-MV=0得:V=![]() v,则知V与v成正比,当木块的速度v最大时,小车的速度V也最大。故C正确。设C与橡皮泥粘在一起时系统的速度为v′,由系统的动量守恒得:(M+m)v′=0,得:v′=0,所以最终系统静止不动,故D错误。故选C。
v,则知V与v成正比,当木块的速度v最大时,小车的速度V也最大。故C正确。设C与橡皮泥粘在一起时系统的速度为v′,由系统的动量守恒得:(M+m)v′=0,得:v′=0,所以最终系统静止不动,故D错误。故选C。

练习册系列答案
相关题目