题目内容
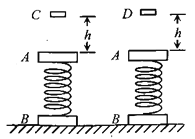
【题目】质量均为M的A、B两个物体由一劲度系数为k的轻弹簧相连，竖直静置于水平地面上，现有两种方案分别都可以使物体A在被碰撞后的运动过程中，物体B恰好能脱离水平地面，这两种方案中相同的是让一个物块从A正上方距A相同高度h处由静止开始自由下落，不同的是不同物块C、D与A发生碰撞种类不同．如题9图所示，方案一是：质量为m的物块C与A碰撞后粘合在一起；方案二是物体D与A发生弹性碰撞后迅速将D取走．已知量为M，m，k，重力加速度g．弹簧始终处于弹性限度内，不计空气阻力．求：
(1)h大小； (2)C、A系统因碰撞损失的机械能； (3)物块D的质量
大小．
【答案】(1) 
(2) 
(3)
【解析】
试题（1）A静止时，设轻弹簧压缩
有
（1分）
设物体C自由落下h时速度为v, 
得：
（1分）
设物体C与A碰撞并粘合在一起竖直向下运动速度大小为
由动量守恒定律得：
（1分）
B恰好能脱离水平面时，C、A向上运动速度为零
设轻弹簧伸长
，由物体B平衡得：
（1 分） 有
（1分）
说明在物体C与A碰撞并粘合在一起运动至最高处过程中C、A、弹簧系统机械能守恒，且初、末弹性势能相同,有
（1分）
（1分）
联立解得
（1分）
（2）C、A系统因碰撞损失的机械能
（2分）
（3）物体D自由落下h时速度为v, 同理有
（1分）
设物体D与A发生弹性碰撞后速度分别为
、
有
（1分） 
（1分）
解得
（1分）
要使B恰好能脱离水平面，与（1）同理，必有
（1分）
得 
（1分）
即：
得
（2分）
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
