Question

（1）如图所示，一横波的波源在坐标原点，x轴为波的传播方向，y轴为振动方向．当波源开始振动0.5s时形成了如图所示的波形（波刚传到图中P点）．则：该波的振幅为

 

；波从图示位置传到Q点所用时间为

 

；Q点开始振动的方向为

 

（2）在水面上放置一个足够大的遮光板，板上有一个半径为r的圆孔，圆心的正上方h处放一个点光源S，在水面下深H处的底部形成半径为R的圆形光亮区域（图中未画出）．测得r=8cm，h=6cm，H=24cm，R=26cm，求水的折射率．

Answer 1

分析：（1）振幅是振动质点离开平衡位置的最大距离，等于y的最大值，由图直接读出．由题确定周期，读出波长，即可由波速公式v=

λ

T

求出波速．根据PQ间的距离，由公式t=

s

v

求时间．Q点开始振动的方向与图示时刻P的振动方向相同．
（2）作出光路图，由几何知识求出入射角和折射角的正弦，再由折射定律求折射率．

解答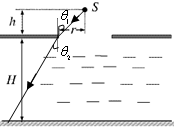：解：（1）该波的振幅为：A=10cm；
由题知：该波的周期为T=0.5s，波长λ=2m，则波速v=

λ

T

=4m/s．
则波从图示位置传到Q点所用时间为t=

PQ

v

=2.5s；
Q点开始振动的方向与图示时刻P的振动方向相同，波向右传播，则由波形的平移法可知：Q点开始振动的方向为沿y轴的负方向．
（2）根据光路图，可知：sinθ1=

r

r2+h2

=

8

82+62

=0.8
sinθ2=

R-r

(R-r)2+H2

=

18

182+242

=0.6
由折射定律得：n=

sinθ1

sinθ2

，得：n=

4

3

故答案为：
（1）10cm，2.5s，沿y轴的负方向．
（2）水的折射率是

4

3

．

点评：小题（1）考查对波动图象和波动规律的理解能力．小题（2）考查对光的折射定律的理解能力和光路图的作图能力．