题目内容
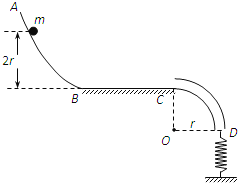
【题目】如图所示,一质量m=1kg的滑块(可视为质点)从高度h=0.2m的光滑斜面的顶端A处由静止滑下, 斜面的底端B与水平传送带平滑相接(滑块经过连接处的能量损失可忽略不计)。已知传送带匀速运行的速度为v0=3m/s,B点到传送带右端C点的距离为L=2m。当滑块滑到传送带的右端C时,其速度恰好与传送带的速度相同。(g取10m/s2)求:
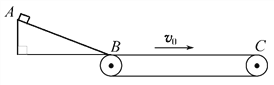
(1)滑块到达底端B速度大小。
(2)滑块与传送带间的动摩擦因数μ。
(3)此过程中,滑块与传送带之间由摩擦而产生的热量Q。
【答案】(1)2m/s (2)0.125 (3)0.5J
【解析】试题分析:滑块从A运动到B的过程中,只有重力做功,根据机械能守恒定律求出滑块到达底端B时的速度;滑块滑上传送带后向右做匀加速运动,滑块在从A到C整个运动过程中,由动能定理即可求出动摩擦因数;根据运动学公式求出滑块从B到C的运动时间,即可求出此时间内传送带的位移,得到滑块与传送带的相对位移,摩擦而产生的热量Q等于滑动摩擦力与相对位移大小的乘积。
(1)滑块由A到B的过程中,由机械能守恒定律得:![]()
解得:vB= 2m/s
(2)滑块从A到C整个运动过程中,由动能定理得:
![]()
代入数据解得:μ=0.125
(3)滑块从B到C运动过程中,设运动时间为t
由运动学公式得:v0=vB+at,其中a=μg
代入数据解得:t=0.8s
在此过程中传送带走的距离为:![]()
则产生的热量: ![]() (1分)
(1分)
代入数据解得:Q=0.5J

 阅读快车系列答案
阅读快车系列答案【题目】在做“研究匀变速直线运动”的实验中:
(1)如图所示,是某同学由打点计时器得到的表示小车运动过程的一条清晰纸带,纸带上两相邻计数点间还有四个点没有画出,打点计时器打点的时间间隔T=0.02 s,其中x1=7.05 cm、x2=7.68 cm、x3=8.33 cm、x4=8.95 cm、x5=9.61 cm、x6=10.26 cm.
![]()
下表列出了打点计时器打下B、C、F时小车的瞬时速度,请在表中填入打点计时器打下D、E两点时小车的瞬时速度.
位置 | B | C | D | E | F |
速度(m·s-1) | 0.737 | 0.801 | ___ | ___ | 0.994 |
(2)以A点为计时起点,在坐标图中画出小车的速度-时间关系图线____.
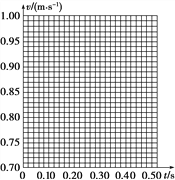
(3)根据你画出的小车的速度-时间关系图线计算出的小车的加速度a=________m/s2.
(4)如果当时电网中交变电流的频率是f=49 Hz,而做实验的同学并不知道,由此引起的系统误差将使加速度的测量值比实际值偏________.(选填“大”或“小”)