Question

【题目】一玻璃砖的截面形状如图所示，其中OAB为半径r的 圆，OBED为矩形，其中矩形的宽BE= r，一细光束以与OB成45°的方向射向圆心O，光束恰好在AD边界发生全反射，之后经DE边反射后从AB边上的N点射出．已知光在真空中的传播速度为c．求：
①光束由N点射出时的折射角；
②光束在玻璃砖中传播的时间．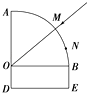

Answer 1

【答案】解：①作出光路图如图所示．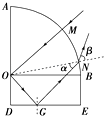

根据几何关系可知，临界角为
C=∠MOB=45°
sinC=
得：n= =
又OD= r，OG= × r= r
根据几何关系可知△OGN是直角三角形，则
sinα= =
根据折射定律有n=
解得：sinβ= ，β=45°
②光束在玻璃砖中的传播速度为：v= =
由几何知识得，光束在玻璃砖中传播的距离为：l=r+ r+
则光束在玻璃砖中传播的时间为：t= =
答：①光束由N点射出时的折射角是45°；
②光束在玻璃砖中传播的时间
【解析】（1）先作出光路图，根据几何关系得出临界角，由全反射临界角公式sinC= 求出折射率n．由几何知识求得光线在F点的入射角，由折射定律求解光束由N点射出时的折射角．（2）光在棱镜中的传播速度v= ．由几何知识求出光线在棱镜中传播的距离S，由t= 求解传播的时间．
【考点精析】利用光的折射对题目进行判断即可得到答案，需要熟知光由一种介质射入另一种介质时，在两种介质的界面上将发生光的传播方向改变的现象叫光的折射．