Question

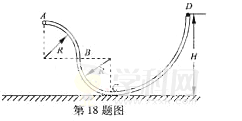
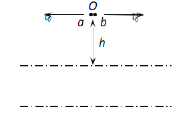
【题目】如图所示，两水平面（虚线）之间的区域存在方向水平向右的匀强电场。从离该区域上边界高为h的O点，沿平行于电场的方向，以相同的速率分别先后向左、右抛出a、b两个小球。a、b两小球均带正电，且质量均为m，a球带电量为βq，b球带电量为q。两小球到达电场上边界的位置之间的距离为L，b球进入电场后在电场中做直线运动。忽略a、b之间的库仑力，重力加速度为g。求：

（1）两小球抛出时速度v0的大小；

（2）若β＝1，且a球进入电场的位置与离开电场的位置在同一竖直线上，求电场上下边界之间的距离；

（3）若电场的上下边界之间的距离为3h，β为何值时可使两小球从同一位置离开电场。

Answer 1

【答案】（1）；（2）8h；（3）7。

【解析】

（1）两球进入电场前均做平抛运动，则：

解得

（2）b球进入电场后在电场中做直线运动，则合力与速度方向共线，即

a球进入电场的位置与离开电场的位置在同一竖直线上，则a球在电场中运动的时间

则电场上下边界间距：

（3）若电场的上下边界之间的距离为 3h，则根据

可得a球离开电场的位置距离O点正下方

B球在电场中运动的时间

对b球在电场中水平方向：

解得

而

解得

β=7

即当β=7时可使两小球从同一位置离开电场。