题目内容
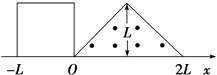
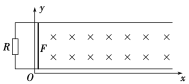
【题目】如图所示，两根相距为L＝1m的足够长的平行光滑金属导轨，位于水平的xOy平面内，一端接有阻值为R＝6Ω的电阻。在x>0的一侧存在垂直纸面向里的磁场，磁感应强度B只随t的增大而增大，且它们间的关系为B＝kt，其中k＝4T/s。一质量为m＝0．5kg的金属杆与金属导轨垂直，可在导轨上滑动，当t＝0时金属杆静止于x＝0处，有一大小可调节的外力F作用于金属杆，使金属杆以恒定加速度a＝2m/s2沿x轴正向做匀加速直线运动。除电阻R以外其余电阻都可以忽略不计。求：当t＝4s时施加于金属杆上的外力为多大。
【答案】513N
【解析】t＝4s时，金属杆移动的位移x＝
at2＝
×2×16m＝16m
此时的速度v＝at＝2×4m/s＝8m/s
切割产生的动生电动势E1＝BLv＝ktLv＝4×4×1×8V＝128V
磁场变化产生的感生电动势E2＝
Lx＝4×1×16V＝64V
根据楞次定律和右手定则知，两个电动势的方向相同
则总电动势E＝E1＋E2＝192V
则感应电流的大小I＝
＝32A
根据牛顿第二定律得，F－BIL＝ma
解得F＝BIL＋ma＝4×4×32×1＋0．5×2N＝513N
练习册系列答案
相关题目
