题目内容
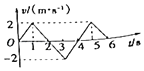
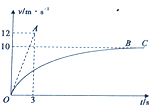
【题目】如图所示,质量m=75kg的滑雪运动员在倾角θ=37°的直滑道上由静止开始向下滑行的速度—时间图象,图中的OA直线是t=0时刻速度图线的切线,速度图线末段BC平行于时间轴,运动员与滑道间的动摩擦因数为μ,所受空气阻力与速度成正比,比例系数为k。设最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,则
A. 物体开始时做加速度增大的加速直线运动,最后做匀速运动
B. t=0时刻运动员的加速度大小为2m/s2
C. 动摩擦因数μ为0.25
D. 比例系数k为15kg/s
【答案】C
【解析】由速度-时间图像可知,物体开始时做加速度减小的加速直线运动,最后做匀速运动,故A错误;在t=0时刻,图线切线的斜率即为该时刻的加速度,故有![]() ,故B错误;在t=0时刻开始加速时,v0=0,由牛顿第二定律可得
,故B错误;在t=0时刻开始加速时,v0=0,由牛顿第二定律可得![]() ,最后匀速时有:vm=10m/s,a=0,由平衡条件可得
,最后匀速时有:vm=10m/s,a=0,由平衡条件可得![]() ,联立解得: μ=0.25,k=30kg/s,故C正确、D错误。所以C正确,ABD错误。
,联立解得: μ=0.25,k=30kg/s,故C正确、D错误。所以C正确,ABD错误。

练习册系列答案
相关题目
【题目】在“探究弹力和弹簧伸长的关系”时,某同学把两根弹簧如图1连接起来进行探究.

(1)某次测量如图2,指针示数为 cm.
(2)在弹性限度内,将50g的钩码逐个挂在弹簧下端,得到指针A、B的示数LA、LB如表.用表数据计算弹簧I的劲度系数为 N/m(重力加速度g=10m/s2).由表数据 (填“能”或“不能”)计算出弹簧Ⅱ的劲度系数.
钩码数 | 1 | 2 | 3 | 4 |
LA/cm | 15.71 | 19.71 | 23.66 | 27.76 |
LB/cm | 29.96 | 35.76 | 41.51 | 47.36 |