题目内容
(10分)如图所示,半径R=0.9m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=1m的水平面相切于B点,BC离地面高h=0.45m,C点与一倾角为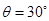 的光滑斜面连接,质量m=1.0kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平面间的动摩擦因数
的光滑斜面连接,质量m=1.0kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平面间的动摩擦因数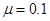 ,取g=10m/s2.
,取g=10m/s2.
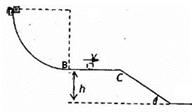
求:(1)小滑块刚到达圆弧的B点时对圆弧的压力:
(2)小滑块到达C点时速度的大小:
(3)小滑块从C点运动到地面所需的时间.
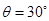 的光滑斜面连接,质量m=1.0kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平面间的动摩擦因数
的光滑斜面连接,质量m=1.0kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平面间的动摩擦因数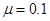 ,取g=10m/s2.
,取g=10m/s2.
求:(1)小滑块刚到达圆弧的B点时对圆弧的压力:
(2)小滑块到达C点时速度的大小:
(3)小滑块从C点运动到地面所需的时间.
(1)30N (2)4m/s (3)0.3s
试题分析:⑴设滑块到B点速度为vB,由机械能守恒
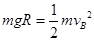 (2分)
(2分)在B点:
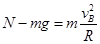 (1分)
(1分)得 N=3mg=30N
由牛顿第三定律,滑块在B点对圆弧的压力大小为30N(1分)
⑵由动能定理,
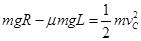 (2分)
(2分)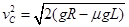 ="4m/s" (1分)
="4m/s" (1分)⑶滑块离开C点后做平抛运动,设其下落h的时间为t,则
由
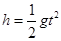
得t=0.3s
t=0.3s内滑块的水平位移x=vct=1.2m(1分)
而斜面的水平长度
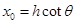 =0.78m
=0.78m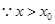 ,所以不会落到斜面上而直接落到地面上,(1分)
,所以不会落到斜面上而直接落到地面上,(1分)所以小滑块从C点运动到地面所需的时间为0.3s(1分)

练习册系列答案
相关题目
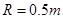 的光滑半圆轨道竖直固定在高
的光滑半圆轨道竖直固定在高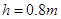 的光滑水平台上,与平台平滑连接,平台长
的光滑水平台上,与平台平滑连接,平台长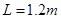 .可视为质点的两物块
.可视为质点的两物块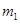 、
、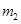 束缚在一起,并静止在平台的最右端D点,它们之间有被压缩的轻质弹簧,某时刻突然解除束缚,使两物块
束缚在一起,并静止在平台的最右端D点,它们之间有被压缩的轻质弹簧,某时刻突然解除束缚,使两物块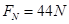 ,水平抛出后在水平地面上的落在水平地面上的P点,
,水平抛出后在水平地面上的落在水平地面上的P点,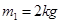 ,
,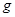 取
取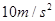 .求:
.求: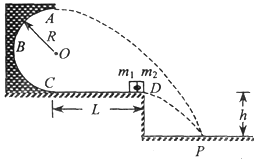
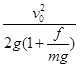 和
和
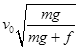
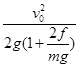 和
和

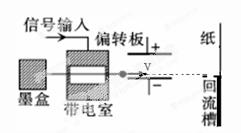

 B.
B. 
 D.
D.