��Ŀ����
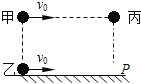
����Ŀ��һ���飨����Ϊ�ʵ㣩��ˮƽ���AB������ֱƽ���ڵ��ķ�֮һ�⻬Բ���ι��BC����֪���������m=0.60kg�����龭��A��ʱ���ٶ�vA=5.0m/s��AB��x=4.5m��������ˮƽ�����Ķ�Ħ��������=0.10��Բ���ι���İ뾶R=0.60m��ȡg=10m/s2����

��1�����龭��B��ʱ�ٶȵĴ�С��
��2�����龭��C��ʱ�ٶȵĴ�С��
��3������ոջ���Բ���ι��ʱ����Բ�������B��ѹ���Ĵ�С��
���𰸡���1��4.0 m/s ��2��2.0 m/s ��3��22N
����������1�������A��B���ȼ���ֱ���˶���Ħ����f=��mg����
��ţ�ٵڶ����ɿ�֪������ļ��ٶȴ�С![]()
���˶�ѧ��ʽvB2��vA2 =��2 a x
��û��龭��B��ʱ�ٶȵĴ�СvB= 4.0 m/s
���⣺���ö��ܶ�������-��mgx=mvB2/2-mvA2/2
vB= 4.0 m/s
��2����B�����龭��C��������ߵ�Ĺ����У��ɻ�е���غ㶨��
mgR=![]() mvB2+
mvB2+![]() mvC2
mvC2
��û��龭��C��ʱ�ٶȵĴ�СvC= 2.0 m/s
��3����B�㣬���鿪ʼ��Բ���˶�����ţ�ٵڶ����ɿ�֪
N-mg=m![]()
��ù���Ի����֧����N = 22N
����ţ�ٵ������ɿ�֪������Թ����B��ѹ���Ĵ�СҲΪ22N��

��ϰ��ϵ�д�
 ״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
�����Ŀ