题目内容
如图,一根有质量的金属棒MN,两端用细软导线连接后悬挂于a、b两点。棒的中部处于方向垂直纸面向里的匀强磁场中,棒中通有电流,方向从M流向N,此时悬线上有拉力。为了使拉力等于零,可以
| A.适当减小磁感应强度 |
| B.使磁场反向 |
| C.适当增大电流强度 |
| D.使电流反向 |
C
解析试题分析:根据左手定则,MN受到竖直向上的安培力,悬线上有拉力时说明安培力小于竖直向下的重力,要使悬线上有拉力等于零,需要增大安培力,根据安培力公式 可知C正确。
可知C正确。
考点:左手定则 安培力

如图所示,在一根一端封闭、内壁光滑的直管MN内有一个带正电的小球,空间中充满竖直向下的匀强磁场。开始时,直管水平放置,且小球位于管的封闭端M处。现使直管沿水平方向向右匀速运动,经一段时间后小球到达管的开口端N处。在小球从M到N的过程中
| A.磁场对小球不做功 |
| B.直管对小球做正功 |
| C.小球所受磁场力的方向不变 |
| D.小球的运动轨迹是一直线 |
如图所示,圆形区域内有垂直于纸面向里的匀强磁场,一个带电粒子以速度v从A点沿直径AOB方向射入磁场,经过Δt时间从C点射出磁场,OC与OB成60°角。现将带电粒子的速度变为 v,仍从A点沿原方向射入磁场,不计重力,则粒子在磁场中的运动时间变为
v,仍从A点沿原方向射入磁场,不计重力,则粒子在磁场中的运动时间变为
A. Δt Δt | B.2Δt |
C. Δt Δt | D. Δt Δt |
如图所示,边界OA与OC之间分布有垂直纸面向里的匀强磁场,边界OA上有一粒子源S.某一时刻,从S平行于纸面向各个方向发射出大量带正电的同种粒子(不计粒子的重力及粒子间的相互作用),所有粒子的初速度大小相同,经过一段时间有大量粒子从边界OC射出磁场.已知∠AOC=60°,从边界OC射出的粒子在磁场中运动的最长时间等于T/2(T为粒子在磁场中运动的周期),则从边界OC射出的粒子在磁场中运动的最短时间为( )
| A.T/2 | B.T/4 | C.T/6 | D.T/8 |
如图所示,界面MN与水平地面之间有足够大正交的匀强磁场B和匀强电场E,磁感线和电场线都处在水平方向且互相垂直。在MN上方有一个带正电的小球由静止开始下落,经电场和磁场到达水平地面。若不计空气阻力,小球在通过电场和磁场的过程中,下列说法中正确的是 
| A.小球做匀变速曲线运动 |
| B.小球的电势能保持不变 |
| C.洛伦兹力对小球做正功 |
| D.小球的动能增量等于其电势能和重力势能减少量的总和 |
如图所示,将长度为L的直导线放置在y轴上,当通以大小为I、沿y轴负方向的电流后,测得其受到的安培力大小为F、方向沿x轴正方向。则匀强磁场的磁感应强度可能:
A.沿z轴正方向,大小为 |
B.在xOy平面内,大小为 |
C.在zOy平面内,大小为 |
D.在zOy平面内,大小为 |


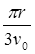
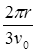


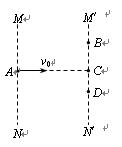
 之间区域内存在着相互垂直的匀强电场和匀强磁场,一带电粒子(不计重力)以初速度v0由A点垂直于MN进入这个区域,带电粒子沿直线运动,并从C点离开场区。如果撤去磁场,该粒子将从B点离开场区;如果撤去电场,该粒子将从D点离开场区。则下列判断正确的是( )
之间区域内存在着相互垂直的匀强电场和匀强磁场,一带电粒子(不计重力)以初速度v0由A点垂直于MN进入这个区域,带电粒子沿直线运动,并从C点离开场区。如果撤去磁场,该粒子将从B点离开场区;如果撤去电场,该粒子将从D点离开场区。则下列判断正确的是( )