题目内容
1. 如图所示为某兴趣小组设计的球形产品传输装置,一内壁光滑的细管弯成半径R=0.4m的半圆形轨道BC,轨道竖直放置,其内径略大于小球的直径,水平轨道MB和水平平台CN分别与竖直半圆轨道平滑连接于B点和C点,MB,CN与小球间的动摩擦因式均为μ=0.5,处于自然伸长状态的轻弹簧左端固定在竖直墙上,右端处于B点左侧,将一个质量m=0.4kg的小球放在轻弹簧右侧,用力向左侧推小球将轻弹簧压缩至A处,AB段长为x1=0.5m,由静止释放小球,小球运动到B处时对轨道的压力F=29N,小球最后静止于水平平台CN上某一点,不计空气阻力,g取10m/s2,则
如图所示为某兴趣小组设计的球形产品传输装置,一内壁光滑的细管弯成半径R=0.4m的半圆形轨道BC,轨道竖直放置,其内径略大于小球的直径,水平轨道MB和水平平台CN分别与竖直半圆轨道平滑连接于B点和C点,MB,CN与小球间的动摩擦因式均为μ=0.5,处于自然伸长状态的轻弹簧左端固定在竖直墙上,右端处于B点左侧,将一个质量m=0.4kg的小球放在轻弹簧右侧,用力向左侧推小球将轻弹簧压缩至A处,AB段长为x1=0.5m,由静止释放小球,小球运动到B处时对轨道的压力F=29N,小球最后静止于水平平台CN上某一点,不计空气阻力,g取10m/s2,则(1)小球在AB段运动时摩擦力对小球所做的功为多少;
(2)轻弹簧压缩至A处时所储存的弹性势能为多少;
(3)小球静止在离C点多远的位置.
分析 (1)由Wf=-μmgx1求小球在AB段运动时摩擦力对小球所做的功.
(2)对小球在B点受力分析,由牛顿第二定律求解B点时的速度.从A到B由能量守恒定律求解弹性势能.
(3)对整个过程,运用能量守恒定律求解.
解答 解:(1)小球在AB段运动时摩擦力对小球所做的功为:
Wf=-μmgx1=-0.5×0.4×10×0.5J=-1J
(2)设小球在B处的速度为v,由牛顿第二定律有:
F-mg=m$\frac{{v}^{2}}{R}$
据题有:F=29N
解得 v=5m/s.
设弹簧在压缩至A点时所储存的弹性势能Ep.
从A到B,能量守恒定律有:
Ep=-Wf+$\frac{1}{2}$mv2
解得:Ep=6J
(3)设小球静止在离C点x m处的位置.
对整个过程,由能量守恒定律得:
Ep=-Wf+μmgx+2mgR
解得 x=0.9m
答:(1)小球在AB段运动时摩擦力对小球所做的功为-1J;
(2)轻弹簧压缩至A处时所储存的弹性势能为6J;
(3)小球静止在离C点0.9m的位置.
点评 了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.一个题目可能需要选择不同的过程多次运用能量守恒或动能定理研究.

练习册系列答案
相关题目
9. 如图所示,一人划小船在河中游玩,当他划至河中间时,发现在他下游60m处时危险区域.而他现在距离两边河岸的距离都为80m,已知各处河水的速度都为3m/s,则要使他能够不至于进入危险区域,他划船的速度至少为( )
如图所示,一人划小船在河中游玩,当他划至河中间时,发现在他下游60m处时危险区域.而他现在距离两边河岸的距离都为80m,已知各处河水的速度都为3m/s,则要使他能够不至于进入危险区域,他划船的速度至少为( )
 如图所示,一人划小船在河中游玩,当他划至河中间时,发现在他下游60m处时危险区域.而他现在距离两边河岸的距离都为80m,已知各处河水的速度都为3m/s,则要使他能够不至于进入危险区域,他划船的速度至少为( )
如图所示,一人划小船在河中游玩,当他划至河中间时,发现在他下游60m处时危险区域.而他现在距离两边河岸的距离都为80m,已知各处河水的速度都为3m/s,则要使他能够不至于进入危险区域,他划船的速度至少为( )| A. | 4m/s | B. | 3m/s | C. | 2.4m/s | D. | 1.8m/s |
16.总质量约为3.8吨“嫦娥三号”探测器在距月面3m处关闭反推发动机,让其以自由落体方式降落在月球表面.4条着陆腿触月信号显示,“嫦娥三号”完美着陆月球虹湾地区.月球表面附近重力加速度约为1.6m/s2,4条着陆腿可视作完全相同的四个轻弹簧,在软着陆后,每个轻弹簧获得的弹性势能大约是( )
| A. | 28500J | B. | 4560J | C. | 18240J | D. | 9120J |
4. 电梯的顶部挂一个弹簧秤,秤下端挂了一个重物,电梯匀速直线运动时,弹簧秤的示数为10N,在某时刻电梯中的人观察到弹簧秤的示数变为6N,关于电梯和重物(如图所示),以下说法正确的是(g取10m/s2)( )
电梯的顶部挂一个弹簧秤,秤下端挂了一个重物,电梯匀速直线运动时,弹簧秤的示数为10N,在某时刻电梯中的人观察到弹簧秤的示数变为6N,关于电梯和重物(如图所示),以下说法正确的是(g取10m/s2)( )
 电梯的顶部挂一个弹簧秤,秤下端挂了一个重物,电梯匀速直线运动时,弹簧秤的示数为10N,在某时刻电梯中的人观察到弹簧秤的示数变为6N,关于电梯和重物(如图所示),以下说法正确的是(g取10m/s2)( )
电梯的顶部挂一个弹簧秤,秤下端挂了一个重物,电梯匀速直线运动时,弹簧秤的示数为10N,在某时刻电梯中的人观察到弹簧秤的示数变为6N,关于电梯和重物(如图所示),以下说法正确的是(g取10m/s2)( )| A. | 重物处在超重状态,电梯可能向上加速运动,加速度大小为4m/s2 | |
| B. | 重物处在超重状态,电梯可能向下加速运动,加速度大小为4m/s2 | |
| C. | 重物处在失重状态,电梯可能向上减速运动,加速度大小为4m/s2 | |
| D. | 重物处在失重状态,电梯可能向下减速运动,加速度大小为4m/s2 |
 如图所示,正方形光滑水平台面WXYZ边长L=1.8m,距地面高h=0.8m.CD线平行于WX边,且它们间距d=0.1m.一个质量为m的微粒从W点静止释放,在WXDC平台区域受到一个从W点指向C点的恒力F1=1.25×10-11N作用,进入CDYZ平台区域后,F1消失,受到另一个力F2作用,其大小满足F2=Kv(v是其速度大小,K=5×10-13Ns/m),运动过程中其方向总是垂直于速度方向,从而在平台上做匀速圆周运动,然后由XY边界离开台面,(台面以外区域F2=0).微粒均视为质点,取g=10m/s2
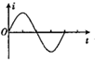
如图所示,正方形光滑水平台面WXYZ边长L=1.8m,距地面高h=0.8m.CD线平行于WX边,且它们间距d=0.1m.一个质量为m的微粒从W点静止释放,在WXDC平台区域受到一个从W点指向C点的恒力F1=1.25×10-11N作用,进入CDYZ平台区域后,F1消失,受到另一个力F2作用,其大小满足F2=Kv(v是其速度大小,K=5×10-13Ns/m),运动过程中其方向总是垂直于速度方向,从而在平台上做匀速圆周运动,然后由XY边界离开台面,(台面以外区域F2=0).微粒均视为质点,取g=10m/s2 如图所示,虚线上方空间有垂直线框平面的匀强磁场,直角扇形导线框绕垂直于线框平面的轴O以角速度ω逆时针匀速转动,若线框中感应电流的方向以逆时针为正,那么在选项中能正确表示线框从图中所示位置开始转动一周的过程中,线框内感应电流随时间变化关系的是( )
如图所示,虚线上方空间有垂直线框平面的匀强磁场,直角扇形导线框绕垂直于线框平面的轴O以角速度ω逆时针匀速转动,若线框中感应电流的方向以逆时针为正,那么在选项中能正确表示线框从图中所示位置开始转动一周的过程中,线框内感应电流随时间变化关系的是( )


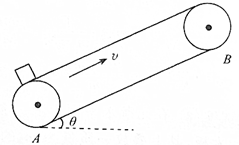 如图所示,有一与水平面成θ角的传送带AB,长度为L,以恒定速率v向上传送,现在A端放上质量为m的物体,物体与皮带间的滑动摩擦系数为μ(摩擦力足以使物体上升),则物体到达B端的时间为多少?若要时间最短,则传动带速率至少应为多少?
如图所示,有一与水平面成θ角的传送带AB,长度为L,以恒定速率v向上传送,现在A端放上质量为m的物体,物体与皮带间的滑动摩擦系数为μ(摩擦力足以使物体上升),则物体到达B端的时间为多少?若要时间最短,则传动带速率至少应为多少?