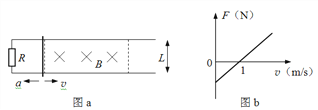��Ŀ����
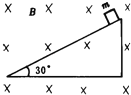
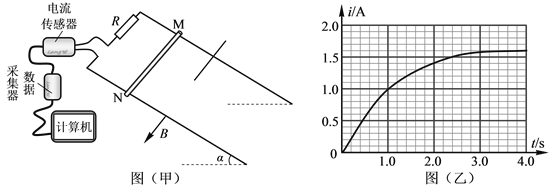
����Ŀ����ͼ���ף���ʾ���������30�㡢����L��0.5m�����費�ƵĹ⻬��������㹻�����ڹ�����϶�������ֵR��1.0���Ķ�ֵ���裬������MN�ĵ���r��0.5��������m��0.16kg������װ�ô��ڴ�ֱ���ƽ�����µ���ǿ�ų��С����������ɾ�ֹ��ʼ�ͷţ��ڼ������Ļ��ͬ����ʾ������i��ʱ��t�Ĺ�ϵ��ͼ���ң���ʾ����֪t��3.2s֮�����������ij���㶨����ֵ��������ʼ�ձ��ִ�ֱ��0~3.2s�ڽ������»��ľ���s��11m����
��1��t��2.0sʱ����R�еĹ��ʣ�
��2���Ÿ�Ӧǿ��B�Ĵ�С��
��3������1.0s~2.0s��ͨ������R�ĵ�����
��4��Ϊ�����0��3.2s�ڻ�·�в����ܵĽ����ȣ�ijͬѧ�ⷨ���£�
��ͼ�õ�t��3.2sʱ����I��1.6A���˹��̵�ƽ������![]() ��
��![]() I��0.8A������
I��0.8A������![]() 2Rt�������R�еĵ��ȣ����������·�����Ľ����ȡ�
2Rt�������R�еĵ��ȣ����������·�����Ľ����ȡ�
��ͬѧ�ⷨ�Ƿ���ȷ������ȷ���������������粻��ȷ����ָ������֮����������ȷ�ķ�����������
���𰸡���1��1.96W����2��1T����3��1.22C����1.20C~1.24C֮���ھ���ȷ������4������ȷ��6.96J
���������������������ͼ����t=2sʱ��·�е������ɹ�ʽP=I2R���������R���ȹ��ʣ�����ͼ��ȡ�����˴ﵽ�ȶ��˶�ʱ�ĵ�������ʱ������ƽ�⣬��ƽ�������Ͱ�������ʽ���Ÿ�Ӧǿ��B�Ĵ�С��ͨ������ĵ�������ͼ����t���Χ�������С�������ͼ������Χ��������������ͨ������ĵ���������������Ա仯����![]() ��⽹����Ҳ����ȷ��Ӧ���������غ���⡣
��⽹����Ҳ����ȷ��Ӧ���������غ���⡣
��1����itͼ���֪��t��2.0sʱI��1.4A������P��I2R��1.96W
��2����ͼ֪���������ȶ��˶�ʱ�ĵ���Ϊ1.60A������������֧������������������ƽ�⣬����ƽ�ⷽ�̵ã�mgsin����BIL��
��ã� ![]()
��3��1.0s ~ 2.0s��ͨ������R�ĵ�����Ӧͼ����t���Χ�ġ����������ͼ֪���ܸ���ԼΪ61��q��61��0.2��0.1��1.22C
��4������ȷ������������Ա仯�� ![]() ����
����![]() ��⽹����Ҳ����ȷ����ȷ��������ͼ֪��3.2s����I��1.60A���綯��E��BLv��I(R+r)���������3.2sʱ�˵��ٶ�
��⽹����Ҳ����ȷ����ȷ��������ͼ֪��3.2s����I��1.60A���綯��E��BLv��I(R+r)���������3.2sʱ�˵��ٶ�![]() ���������ݽ�ã�v��4.8m/s
���������ݽ�ã�v��4.8m/s
�����غ㣺 ![]() ������ܵĽ�����Ϊ��
������ܵĽ�����Ϊ�� ![]()
�������ݽ�ã� ![]()