题目内容
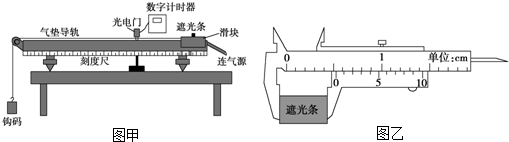
10.某同学为了测定一长木板和铁块之间的动摩擦因数,将长木板放在水平桌面上,并且将长木板的一端用铁架台支起一定的高度,组成如图(1)所示装置(示意图),使铁块加速下滑.所提供的仪器有长木板、铁块、打点计时器(含纸带)、学生电源、米尺、铁架台及导线、开关等.图(2)是打点计时器打出的一条纸带,纸带上标注了几个计数点,若相邻两个计数点间的时间间隔均为T,计数点间距离分别为S1、S2、S3、S4,则: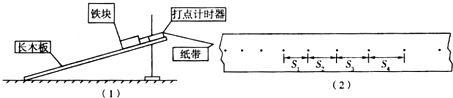
(1)将长木板的一端支起是为了使铁块加速下滑
(2)由纸带求出铁块下滑的加速度的大小a=$\frac{({s}_{4}+{s}_{3})-({s}_{1}+{s}_{2})}{4{T}^{2}}$
(3)为了测定铁块与长木板间的动摩擦因数,该同学还测量了长木板右端被支起的高度h和长木板的长度L,设加速度a、重力加速度g,则动摩擦因数的计算式是μ=$\frac{gh-aL}{g\sqrt{{L}^{2}-{h}^{2}}}$(用字母h、L、a和g表示).
分析 (1)根据题意明确实验原理,则可得出将长木板支起的目的;
(2)由逐差法可求得加速度的大小;
(3)根据牛顿第二定律可求得摩擦力与加速度间的关系,再由角边关系列式,联立可求得动摩擦因数.
解答 解:(1)本实验是通过物体的运动来测量动摩擦因数,故将木板一端支起的目的是将铁块加速下滑;
(2)由逐差法可得:
s3-s1=2aT2;
s4-s2=2aT2;
联立解得:
a=$\frac{({s}_{4}+{s}_{3})-({s}_{1}+{s}_{2})}{4{T}^{2}}$;
(3)由牛顿第二定律可得:
mgsinθ-μmgcosθ=ma
由几何关系可知:
sinθ=$\frac{h}{L}$;
cosθ=$\frac{\sqrt{{L}^{2}-{h}^{2}}}{L}$;
联立解得:
μ=$\frac{gh-aL}{g\sqrt{{L}^{2}-{h}^{2}}}$
故答案为:(1)使铁块加速下滑;(2)$\frac{({s}_{4}+{s}_{3})-({s}_{1}+{s}_{2})}{4{T}^{2}}$;(3)$\frac{gh-aL}{g\sqrt{{L}^{2}-{h}^{2}}}$
点评 本题通过动能定理得出动摩擦因数的表达式,从而确定要测量的物理量.要先确定实验的原理,然后依据实验的原理解答即可.

练习册系列答案
相关题目
18.下列说法正确的是( )
| A. | 正负电子对碰撞过程动量不守恒 | |
| B. | 人工放射性同位素比天然放射性同位素半衰期长的多,因此废料不容易处理 | |
| C. | 实物粒子也具有波动性,每一种运动粒子都有一个对应的波相联系 | |
| D. | 太阳辐射的能量主要来自太阳内部的重核裂变释放的核能 |
15.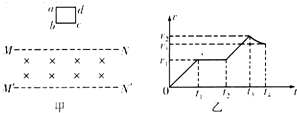 如图甲所示,正方形金属线圈abcd位于竖直平面内,其质量为m,电阻为R.在线圈的下方有一匀强磁场,MN和M′N′是磁场的水平边界,并与bc边平行,磁场方向垂直于纸面向里.现使金属线框从MN上方某一高度处由静止开始下落,图乙是线圈由开始下落到完全穿过匀强磁场区域瞬间的v-t图象,图中字母均为已知量.重力加速度为g,不计空气阻力.下列说法正确的是( )
如图甲所示,正方形金属线圈abcd位于竖直平面内,其质量为m,电阻为R.在线圈的下方有一匀强磁场,MN和M′N′是磁场的水平边界,并与bc边平行,磁场方向垂直于纸面向里.现使金属线框从MN上方某一高度处由静止开始下落,图乙是线圈由开始下落到完全穿过匀强磁场区域瞬间的v-t图象,图中字母均为已知量.重力加速度为g,不计空气阻力.下列说法正确的是( )
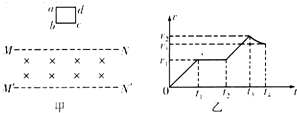 如图甲所示,正方形金属线圈abcd位于竖直平面内,其质量为m,电阻为R.在线圈的下方有一匀强磁场,MN和M′N′是磁场的水平边界,并与bc边平行,磁场方向垂直于纸面向里.现使金属线框从MN上方某一高度处由静止开始下落,图乙是线圈由开始下落到完全穿过匀强磁场区域瞬间的v-t图象,图中字母均为已知量.重力加速度为g,不计空气阻力.下列说法正确的是( )
如图甲所示,正方形金属线圈abcd位于竖直平面内,其质量为m,电阻为R.在线圈的下方有一匀强磁场,MN和M′N′是磁场的水平边界,并与bc边平行,磁场方向垂直于纸面向里.现使金属线框从MN上方某一高度处由静止开始下落,图乙是线圈由开始下落到完全穿过匀强磁场区域瞬间的v-t图象,图中字母均为已知量.重力加速度为g,不计空气阻力.下列说法正确的是( )| A. | 金属线框刚进入磁场时感应电流方向沿adcba方向 | |
| B. | 金属线框的边长为v1(t2-t1) | |
| C. | 磁场的磁感应强度为$\frac{1}{{{v_1}({{t_1}-{t_2}})}}\sqrt{\frac{mgR}{v_1}}$ | |
| D. | 金属线框在0~t4的时间内所产生的热量为2mgV1(t2-t1)+$\frac{1}{2}$m(V22-V32) |
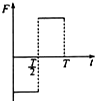
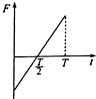
2.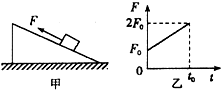 在图甲所示的粗糙斜面上,用平行于斜面向上的拉力F拉物块,斜面和物块始终处于静止状态.若拉力F按图乙所示规律变化,下列判断正确的是( )
在图甲所示的粗糙斜面上,用平行于斜面向上的拉力F拉物块,斜面和物块始终处于静止状态.若拉力F按图乙所示规律变化,下列判断正确的是( )
 在图甲所示的粗糙斜面上,用平行于斜面向上的拉力F拉物块,斜面和物块始终处于静止状态.若拉力F按图乙所示规律变化,下列判断正确的是( )
在图甲所示的粗糙斜面上,用平行于斜面向上的拉力F拉物块,斜面和物块始终处于静止状态.若拉力F按图乙所示规律变化,下列判断正确的是( )| A. | 地面对斜面的摩擦力逐渐减小 | B. | 地面对斜面的摩擦力逐渐增大 | ||
| C. | 物块对斜面的摩擦力可能一直增大 | D. | 物块对斜面的摩擦力可能一直减小 |
19.一质点在外力作用下由静止开始作直线运动,其v-t图象如图所示,该质点( )


| A. | 在0~1s内做加速度增大的加速运动 | B. | 在第1s末速度方向发生了变化 | ||
| C. | 在t=1.5s时离出发点最远 | D. | 在1.5~2.5s内做匀减速直线运动 |
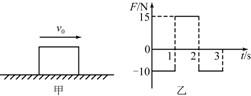 如图甲所示,一质量m=2.5kg的物块在粗糙的水平地面上向右运动,当速度v0=20m/s时,施加一水平外力F,外力F随时间t的变化关系如图乙所示.外力F作用3s后撤去,规定水平向右为正方向,已知物块与地面间的动摩擦因数μ=0.4,重力加速度g=10m/s2.求:
如图甲所示,一质量m=2.5kg的物块在粗糙的水平地面上向右运动,当速度v0=20m/s时,施加一水平外力F,外力F随时间t的变化关系如图乙所示.外力F作用3s后撤去,规定水平向右为正方向,已知物块与地面间的动摩擦因数μ=0.4,重力加速度g=10m/s2.求:
 通电直导线周围的某点磁感应强度B的大小与该点到直导线的距离成反比,与通电直导线中的电流的大小成正比,可以用公式B=k$\frac{I}{r}$来表示,其中k为比例常数,俯视图如图所示,在光滑水平面上有一通电直导线ab,旁边有一矩形金属线框cdef,cd边与导线ab平行,当导线ab中通如图所示电流时(设a流向b为电流的正方向),为使矩形金属线框cdef静止不动,需加一水平方向的力F(设向右为正方向),则正确的是( )
通电直导线周围的某点磁感应强度B的大小与该点到直导线的距离成反比,与通电直导线中的电流的大小成正比,可以用公式B=k$\frac{I}{r}$来表示,其中k为比例常数,俯视图如图所示,在光滑水平面上有一通电直导线ab,旁边有一矩形金属线框cdef,cd边与导线ab平行,当导线ab中通如图所示电流时(设a流向b为电流的正方向),为使矩形金属线框cdef静止不动,需加一水平方向的力F(设向右为正方向),则正确的是( )