题目内容
5.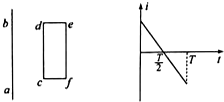 通电直导线周围的某点磁感应强度B的大小与该点到直导线的距离成反比,与通电直导线中的电流的大小成正比,可以用公式B=k$\frac{I}{r}$来表示,其中k为比例常数,俯视图如图所示,在光滑水平面上有一通电直导线ab,旁边有一矩形金属线框cdef,cd边与导线ab平行,当导线ab中通如图所示电流时(设a流向b为电流的正方向),为使矩形金属线框cdef静止不动,需加一水平方向的力F(设向右为正方向),则正确的是( )
通电直导线周围的某点磁感应强度B的大小与该点到直导线的距离成反比,与通电直导线中的电流的大小成正比,可以用公式B=k$\frac{I}{r}$来表示,其中k为比例常数,俯视图如图所示,在光滑水平面上有一通电直导线ab,旁边有一矩形金属线框cdef,cd边与导线ab平行,当导线ab中通如图所示电流时(设a流向b为电流的正方向),为使矩形金属线框cdef静止不动,需加一水平方向的力F(设向右为正方向),则正确的是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据感应电动势E=$\frac{N△∅}{△t}$,结合安培力表达式F=BIL,及平衡条件,从而确定外力与时间变化关系式,进而即可求解.
解答 解:由图,结合感应电动势表达式,可知,在线圈中产生的感应电流恒定,
根据安培定则与楞次定律可知,感应电流方向顺时针方向,
那么由左手定则可知,矩形金属线框安培力的合力的方向先向左,后向右;
再由平衡条件,可得,外力的方向先右后向左,
对于安培力大小随着通入ab的电流先减小,后增大,
因此外力的大小也是先减小,后反向增大,故C正确,ABD错误;
故选:C.
点评 考查安培定则、楞次定律与法拉第电磁感应定律的应用,掌握安培力方向判定,注意左手定则与右手定则的区别,及理解平衡的条件的应用.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
14.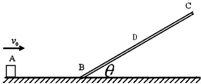 如图,BC为长度一定可以绕B点转动调节倾角大小的斜面,AB为水平面,刚开始时,斜面倾角为45°,一可视为质点的小滑块从A点出发向左运动冲上斜面,初速度大小为v0,恰好能到达斜面中点D,已知物块与斜面和水平面的滑动摩擦因素均为μ=1,不计物块由水平面进入斜面瞬间的能量损失,下列说法正确的是( )
如图,BC为长度一定可以绕B点转动调节倾角大小的斜面,AB为水平面,刚开始时,斜面倾角为45°,一可视为质点的小滑块从A点出发向左运动冲上斜面,初速度大小为v0,恰好能到达斜面中点D,已知物块与斜面和水平面的滑动摩擦因素均为μ=1,不计物块由水平面进入斜面瞬间的能量损失,下列说法正确的是( )
 如图,BC为长度一定可以绕B点转动调节倾角大小的斜面,AB为水平面,刚开始时,斜面倾角为45°,一可视为质点的小滑块从A点出发向左运动冲上斜面,初速度大小为v0,恰好能到达斜面中点D,已知物块与斜面和水平面的滑动摩擦因素均为μ=1,不计物块由水平面进入斜面瞬间的能量损失,下列说法正确的是( )
如图,BC为长度一定可以绕B点转动调节倾角大小的斜面,AB为水平面,刚开始时,斜面倾角为45°,一可视为质点的小滑块从A点出发向左运动冲上斜面,初速度大小为v0,恰好能到达斜面中点D,已知物块与斜面和水平面的滑动摩擦因素均为μ=1,不计物块由水平面进入斜面瞬间的能量损失,下列说法正确的是( )| A. | 保持初速v0不变,逐渐减小斜面倾角,小球不可能到达C点 | |
| B. | 保持初速v0不变,逐渐减小斜面倾角,每次小滑块克服摩擦阻力做的功相等 | |
| C. | 保持斜面倾角不变,初速度变为2v0,小滑块一定能冲过C点 | |
| D. | 保持倾角和初速度不变,滑动摩擦因素μ=0.5时,小滑块一定能冲过C点 |
15.在电梯内的地板上,竖直放置一根轻质弹簧,弹簧上端固定一个质量为m的物体.当电梯匀速运动时,弹簧被压缩了x,某时刻后观察到弹簧又被继续压缩了$\frac{x}{10}$(重力加速度为g).则电梯在此时刻后的运动情况可能是( )
| A. | 以大小为$\frac{11}{10}$g的加速度加速上升 | B. | 以大小为$\frac{11}{10}$g的加速度减速上升 | ||
| C. | 以大小为$\frac{g}{10}$的加速度加速下降 | D. | 以大小为$\frac{g}{10}$的加速度减速下降 |
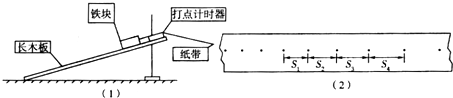
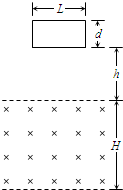 如图所示,有一磁感应强度大小为B的水平匀强磁场,其上下水平边界的间距为H;磁场的正上方有一长方形导线框,其长和宽分别为L、d(d<H),质量为m,电阻为R.现将线框从其下边缘与磁场上边界间的距离为h处由静止释放,测得线框进入磁场的过程所用的时间为t.线框平面始终与磁场方向垂直,线框上下边始终保持水平,重力加速度为g.求:
如图所示,有一磁感应强度大小为B的水平匀强磁场,其上下水平边界的间距为H;磁场的正上方有一长方形导线框,其长和宽分别为L、d(d<H),质量为m,电阻为R.现将线框从其下边缘与磁场上边界间的距离为h处由静止释放,测得线框进入磁场的过程所用的时间为t.线框平面始终与磁场方向垂直,线框上下边始终保持水平,重力加速度为g.求: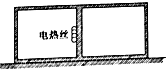 一内壁光滑体积为V的绝热气缸固定在水平地面上,绝热光滑活塞厚度不计,刚开始时处于气缸的中间位置,活塞两侧封闭相同质量的相同理想气体.初始状态两侧温度T0=300K,压强为P0.若活塞左侧气缸内电热丝通电,温度升高到T=600K,试求左侧气缸的压强与体积.
一内壁光滑体积为V的绝热气缸固定在水平地面上,绝热光滑活塞厚度不计,刚开始时处于气缸的中间位置,活塞两侧封闭相同质量的相同理想气体.初始状态两侧温度T0=300K,压强为P0.若活塞左侧气缸内电热丝通电,温度升高到T=600K,试求左侧气缸的压强与体积.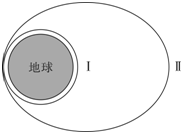 空间站是一种在近地轨道长时间运行,可供多名航天员巡访、长期工作和生活的载人航天器.如图所示,某空间站在轨道半径为R的近地圆轨道 I上围绕地球运行,一宇宙飞船与空间站对接检修后再与空间站分离,分离时宇宙飞船依靠自身动力装置在很短的距离内加速,进入椭圆轨道Ⅱ运行.已知椭圆轨道的远地点到地球球心的距离为3.5R,地球质量为M,万有引力常量为G,求
空间站是一种在近地轨道长时间运行,可供多名航天员巡访、长期工作和生活的载人航天器.如图所示,某空间站在轨道半径为R的近地圆轨道 I上围绕地球运行,一宇宙飞船与空间站对接检修后再与空间站分离,分离时宇宙飞船依靠自身动力装置在很短的距离内加速,进入椭圆轨道Ⅱ运行.已知椭圆轨道的远地点到地球球心的距离为3.5R,地球质量为M,万有引力常量为G,求