题目内容
如图所示，长为L的细绳，一端系着一只小球，另一端悬于O点，将小球由图示位置由静止释放，当摆到O点正下方时，绳被小钉挡住．当钉子分别处于图中A、B、C三个不同位置时，小球继续摆的最大高度分别为h1、h2、h3，则（ ）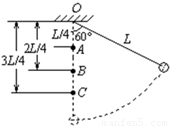
A．h1＞h2＞h3
B．h1=h2=h3
C．h1＞h2=h3
D．h1=h2＞h3
【答案】分析：当光滑小钉位于A、B两处时，由机械能守恒可知，小球将摆到与B等高处，
当光滑小钉位于C处时，根据牛顿第二定律和圆周运动知识得圆周运动最高点B的临界速度．
解答：解：小球的释放点距D点的高度为h=L-Lcos60°=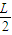
，即与B点等高．
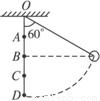
当光滑小钉位于A、B两处时，由机械能守恒可知，小球将摆到与B等高处，即h1=h2；
当光滑小钉位于C处时，假设小球能从释放点到B点，
由机械能守恒可得，到B点时速度vB=0，
根据牛顿第二定律和圆周运动知识得
mg=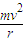
v=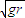
所以要使小球运动到B点，vB≥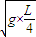
=
，
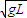所以不能到达B点．所以h1=h2＞h3，
故选D．
点评：该题关键要知道1、小球机械能守恒，2、细线带小球到圆周运动最高点速度大于等于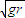
．
当光滑小钉位于C处时，根据牛顿第二定律和圆周运动知识得圆周运动最高点B的临界速度．
解答：解：小球的释放点距D点的高度为h=L-Lcos60°=
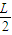，即与B点等高．当光滑小钉位于A、B两处时，由机械能守恒可知，小球将摆到与B等高处，即h1=h2；
当光滑小钉位于C处时，假设小球能从释放点到B点，
由机械能守恒可得，到B点时速度vB=0，
根据牛顿第二定律和圆周运动知识得
mg=
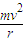
v=
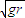
所以要使小球运动到B点，vB≥
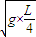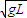=，所以不能到达B点．所以h1=h2＞h3，
故选D．
点评：该题关键要知道1、小球机械能守恒，2、细线带小球到圆周运动最高点速度大于等于
． 
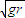练习册系列答案
相关题目
如图所示，长为L的细绳上端系一质量不计的环，环套在光滑水平杆上，在细线的下端吊一个质量为m的铁球（可视作质点），球离地的高度h=L，当绳受到大小为3mg的拉力时就会断裂，现让环与球一起以v=
如图所示，长为L的细绳一端固定，另一端系一质量为m的小球．给小球一个合适的初速度，小球便可在水平面内做匀速圆周运动，这样就构成了个圆锥摆，设细绳与竖直方向的夹角为θ．下列说法中正确的是（ ）
如图所示，长为L的细绳，一端系有一质量为m的小球，另一端固定在O点，细绳能够承受的最大拉力为9mg．现将小球拉至细绳呈水平位置，然后由静止释放，小球将在竖直平面内摆动，不计空气阻力．求：
（2012?杭州模拟）如图所示，长为L的细绳一端固定在O点，另一端拴住一个小球，在O点的正下方与O点相距2L/3的地方有一枚与竖直平面垂直的钉子A；把球拉起使细绳在水平方向伸直，由静止开始释放，当细线碰到钉子后的瞬间（细绳没有断），下列说法正确的是（ ）
如图所示，长为L的细绳，一端系着一只小球，另一端悬于O点，将小球由图示位置由静止释放，当摆到O点正下方时，绳被小钉挡住．当钉子分别处于图中A、B、C三个不同位置时，小球继续摆的最大高度分别为h1、h2、h3，则（ ）